题目内容
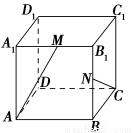
(本小题满分9分)如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.

(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
(1)证明见解析;(2)证明见解析;
【解析】
试题分析:(1)由题可知,证明线面平行主要有3种方法,分别是平行四边形法,三角形中位线法,构造辅助平面法,在本题中,取PD的中点E,连接EN,EA,则四边形ENMA构成了平行四边形,由线线平行即可得出线面平行;(2)由题可知,证明面面垂直常用的方法是通过线面垂直得到,在本题中,由MN⊥平面PCD,MN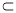 平面PMC,所以得出平面PMC⊥平面PCD;
平面PMC,所以得出平面PMC⊥平面PCD;
试题解析:(1)设PD的中点为E,连结AE、NE,由N为PD的中点知EN
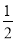 DC,
DC,
又ABCD是矩形,∴DC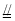 AB,∴EN
AB,∴EN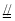
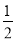 AB,又M是AB的中点,∴EN
AB,又M是AB的中点,∴EN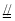 AN,
AN,
∴AMNE是平行四边形
∴MN∥AE,而AE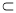 平面PAD,NM
平面PAD,NM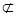 平面PAD ∴MN∥平面PAD (4分)
平面PAD ∴MN∥平面PAD (4分)

(2)∵PA=AD,∴AE⊥PD,又∵PA⊥平面ABCD,CD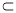 平面ABCD,
平面ABCD,
∴CD⊥PA,而CD⊥AD,∴CD⊥平面PAD
∴CD⊥AE, ∵PD∩CD=D,∴AE⊥平面PCD,
∵MN∥AE,∴MN⊥平面PCD,
又MN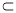 平面PMC,∴平面PMC⊥平面PCD. (9分)
平面PMC,∴平面PMC⊥平面PCD. (9分)
考点:?线面平行的判定定理?面面垂直的判定定理

练习册系列答案
相关题目
 满足:
满足: ,且
,且 是
是 的等差中项.
的等差中项. 的通项公式;
的通项公式; ,
,
 ,求使
,求使 成立的正整数
成立的正整数 的最小值.
的最小值. 的前
的前 项和为
项和为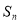 ,若
,若 ,则
,则 等于
等于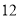 (B)
(B)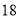 (C)
(C) (D)
(D)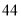
 与直线
与直线 的位置关系是( )
的位置关系是( ) 是锐二面角
是锐二面角 的
的 内一点,
内一点, 于点
于点 到
到 的距离为
的距离为 ,则二面角
,则二面角 的平面角大小为
的平面角大小为 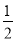 B.m<
B.m<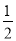 C. m≤
C. m≤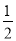 D. m>0
D. m>0 的定义域是 。
的定义域是 。