题目内容
已知椭圆C:
+
=1(a>b>0)的左焦点为F1(-
,0),短轴的端点到右焦点的距离为
.
(1)求椭圆C的方程;
(2)若直线l与圆4x2+4y2=3相切,且与椭圆C交于A,B两点,求|AB|的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
(1)求椭圆C的方程;
(2)若直线l与圆4x2+4y2=3相切,且与椭圆C交于A,B两点,求|AB|的最大值.
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)利用椭圆的性质和b=
即可得出;
(2)当斜率不为0时,设切线的方程为x=my+n.利用点到直线的距离公式可得
=
,再把切线方程与椭圆的方程联立可得根与系数的关系,利用弦长公式可得|AB|.当斜率为0时,直接求出,再比较即可.
| a2-c2 |
(2)当斜率不为0时,设切线的方程为x=my+n.利用点到直线的距离公式可得
| |n| | ||
|
| ||
| 2 |
解答:
解:(1)∵椭圆C:
+
=1(a>b>0)的左焦点为F1(-
,0),短轴的端点到右焦点的距离为
,
∴c=
,a=
,
∴b=
=1,
∴椭圆C的方程为
+y2=1;
(2)①当斜率不为0时,设切线的方程为x=my+n.
则
=
,化为4n2=3+3m2.
联立
,化为(3+m2)y2+2mny+n2-3=0.
∴y1+y2=-
,y1y2=
.
∴|AB|=
=
=
,
把n2=
代入上式可得|AB|=
≤
=2,当且仅当m2=3时取等号.
②当斜率为0时,不妨取xA=
,代入椭圆的方程可得
×(
)2+
=1,解得yA=±
|AB|=
<2.
综上①②可知:|AB|的最大值是2.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
∴c=
| 2 |
| 3 |
∴b=
| a2-c2 |
∴椭圆C的方程为
| x2 |
| 3 |
(2)①当斜率不为0时,设切线的方程为x=my+n.
则
| |n| | ||
|
| ||
| 2 |
联立
|
∴y1+y2=-
| 2mn |
| 3+m2 |
| n2-3 |
| 3+m2 |
∴|AB|=
| (1+m2)[(y1+y2)2-4y1y2] |
(1+m2)[
|
2
| ||
| 3+m2 |
把n2=
| 3+3m2 |
| 4 |
3(1+
|
3(1+
|
②当斜率为0时,不妨取xA=
| ||
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| y | 2 A |
| ||
| 2 |
|AB|=
| 3 |
综上①②可知:|AB|的最大值是2.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立得到的根与系数的关系、弦长公式等基础知识与基本技能方法,考查了分类讨论思想方法、推理能力和计算能力,属于难题.

练习册系列答案
相关题目
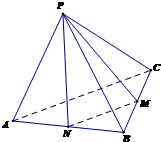 (文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示).
(文科)如图,正四面体P-ABC中,M为线段BC的中点,求异面直线PM与AC所成的角(结果用反三角函数值表示). 如图,在四棱锥S-ABCD中,底面ABCD是正方形,四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC的中点.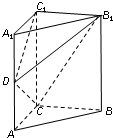 如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2.
如图,在正三棱柱ABC-A1B1C1中,AA1=AB=2. 如图,正方形ABCD与梯形CDEF所在的平面互相垂直,CD⊥DE,CF∥DE,CD=CF=2,DE=4,G为AE的中点.
如图,正方形ABCD与梯形CDEF所在的平面互相垂直,CD⊥DE,CF∥DE,CD=CF=2,DE=4,G为AE的中点.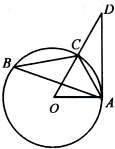 如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为
如图,已知△ABC内接于圆O,点D在OC的延长线上,AD是圆O的切线,若∠OAC=60°,AC=1,则AD的长为