题目内容

16．以直角坐标系的原点为极点，x轴的非负半轴为极轴，建立极坐标系，并在两种坐标系中取相同的长度单位，已知直线l的参数方程为$\left\{\begin{array}{l}x=5-\frac{{\sqrt{3}}}{2}t\\ y=-\sqrt{3}+\frac{1}{2}t\end{array}\right.$（t为参数），圆C的极坐标方程为$ρ=4cos（θ-\frac{π}{3}）$
（I）求直线l和圆C的直角坐标方程；
（Ⅱ）若点P（x，y）在圆C上，求$\sqrt{3}x-y$的取值范围．

分析 （Ⅰ）直线l的参数方程消去参数t，能求出直线l的直角坐标方程；圆C的极坐标方程转化为${ρ}^{2}=2ρcosθ+2\sqrt{3}ρsinθ$，由ρ2=x2+y2，ρcosθ=x，ρsinθ=y，能求出圆C的直角坐标方程．
（Ⅱ）设P（1+2cosθ，$\sqrt{3}+2sinθ$），则$\sqrt{3}x-y$=$\sqrt{3}+2\sqrt{3}cosθ-\sqrt{3}-2sinθ$=4sin（θ+$\frac{2π}{3}$），由此能求出$\sqrt{3}x-y$的取值范围．

解答 解：（Ⅰ）∵直线l的参数方程为$\left\{\begin{array}{l}x=5-\frac{{\sqrt{3}}}{2}t\\ y=-\sqrt{3}+\frac{1}{2}t\end{array}\right.$（t为参数），
∴消去参数t，得直线l的直角坐标方程为x+$\sqrt{3}y$-2=0，
∵圆C的极坐标方程为$ρ=4cos（θ-\frac{π}{3}）$，
∴${ρ}^{2}=2ρcosθ+2\sqrt{3}ρsinθ$，
∵ρ2=x2+y2，ρcosθ=x，ρsinθ=y，
∴圆C的直角坐标方程为（x-1）2+（y-$\sqrt{3}$）2=4．
（Ⅱ）∵点P（x，y）在圆C上，
∴设P（1+2cosθ，$\sqrt{3}+2sinθ$），
∴$\sqrt{3}x-y$=$\sqrt{3}+2\sqrt{3}cosθ-\sqrt{3}-2sinθ$=4sin（θ+$\frac{2π}{3}$），
∴$\sqrt{3}x-y$的取值范围是[-4，4]．

点评 本题考查直线和圆直角坐标方程的求法，考查代数式的取值范围的求法，考查极坐标方程、直角坐标方程、参数方程的互化等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、函数与方程思想，是中档题．

练习册系列答案
相关题目
8．设A（1，1）、B（7，4），点C满足$\overrightarrow{AC}$=2$\overrightarrow{CB}$，则点C的坐标是（　　）
A．（3，2）B．（3，5）C．（5，3）D．（8，5）
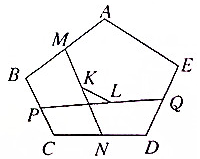7．如图所示，五边形ABC 中，点M、N、P、Q分别是AB、CD、BC、DE的中点，K和L分别是MN和PQ的中点．求证：$\overrightarrow{KL}$=$\frac{1}{4}$$\overrightarrow{AE}$．
4．在等差数列{an}中，a1＜0，S18=S36，若Sn最小，则n的值为（　　）
A．18B．27C．36D．54
11．若不等式组$\left\{\begin{array}{l}{x+a≥0}\\{4-2x＞x-2}\end{array}\right.$有解，则实数a的取值范围是（　　）
A．a≥-2B．a＜-2C．a≤-2D．a＞-2
1．已知等差数列{an}的前5项和为105，且a10=2a5，求数列{an}的通项公式．
8．已知F1，F2为双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的左、右两个焦点，点M在E上，MF1与x轴垂直，sin∠MF2F1=$\frac{1}{3}$，则E的离心率为$\sqrt{2}$．
5．已知四面体ABCD中，∠BAC=60°，∠BAD=∠CAD=90°，$AB=\sqrt{3}$，$AC=2\sqrt{3}$，其外接球体积为$\frac{32}{3}π$，则该四面体ABCD的棱AD=2．
6．已知函数$f（x）=cos（2x+\frac{π}{4}）（x∈R）$，为了得到函数g（x）=cos2x的图象，只要将y=f（x）的图象（　　）
A．向左平移$\frac{π}{4}$个单位长度B．向右平移$\frac{π}{4}$个单位长度
C．向左平移$\frac{π}{8}$个单位长度D．向右平移$\frac{π}{8}$个单位长度

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网