题目内容
8.在△ABC中,角A,B,C的对边分别为a,b,c,若a=4$\sqrt{2}$,b=5,cosA=-$\frac{3}{5}$,则向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为( )| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{7\sqrt{2}}{2}$ | D. | $\frac{7\sqrt{2}}{2}$ |
分析 根据cosA=-$\frac{3}{5}$得出A为钝角,sinA=$\frac{4}{5}$,利用正弦定理求出B,再利用余弦定理求出c,根据向量投影的定义写出运算结果即可.
解答 解:△ABC中,a=4$\sqrt{2}$,b=5,cosA=-$\frac{3}{5}$,
∴A为钝角,且sinA=$\frac{4}{5}$,
∴$\frac{a}{sinA}$=$\frac{b}{sinB}$
sinB=$\frac{bsinA}{a}$=$\frac{5×\frac{4}{5}}{4\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
由题知A>B,故B=$\frac{π}{4}$;
∵a2=b2+c2-2bccosA,
∴(4$\sqrt{2}$)2=52+c2-2•5c•(-$\frac{3}{5}$),
解得c=1或c=-7(舍去),
∴向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为:
|$\overrightarrow{BA}$|cosB=ccos$\frac{π}{4}$=1×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查了平面向量的数量积与正弦、余弦定理的应用问题,是综合性题目.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
1.F是抛物线y2=2x的焦点,以F为端点的射线与抛物线相交于A,与抛物线的准线相交于B,若$\overrightarrow{FB}=4\overrightarrow{FA}$,则$\overrightarrow{FA}•\overrightarrow{FB}$=( )
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{9}{4}$ |
16.如图,某几何体的三视图如图所示,则该几何体的各条棱中最长的棱和最短的棱长度之和为( )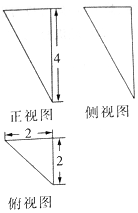

| A. | 6 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{5}$+2 | D. | 2$\sqrt{6}$+2 |
3.实数x,y满足不等式组$\left\{\begin{array}{l}{x≥0}\\{x-y-1≤0}\\{x-2y+1≥0}\end{array}\right.$,则2x-y的最大值为( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
16.已知集合U={1,2,3,4,5,6}M={1,2},N={2,3,4},则M∩(∁UN)=( )
| A. | {1} | B. | {2} | C. | {1,2,5,6} | D. | {1,2,3,4} |
17.设f′(x)、g′(x)分别是函数f(x)、g(x)(x∈R)的导数,且满足g(x)>0,f′(x)g(x)-f(x)g′(x)>0.若△ABC中,∠C是钝角,则( )
| A. | f(sinA)•g(sinB)>f(sinB)•g(sinA) | B. | f(sinA)•g(sinB)<f(sinB)•g(sinA) | ||
| C. | f(cosA)•g(sinB)>f(sinB)•g(cosA) | D. | f(cosA)•g(sinB)<f(sinB)•g(cosA) |