题目内容
3.实数x,y满足不等式组$\left\{\begin{array}{l}{x≥0}\\{x-y-1≤0}\\{x-2y+1≥0}\end{array}\right.$,则2x-y的最大值为( )| A. | -$\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
分析 作出不等式组对应的平面区域,利用目标函数k的几何意义,进行平移,结合图象得到k=2x-y的最大值.
解答 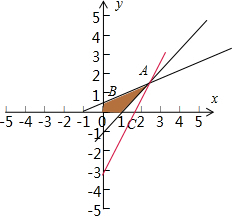 解:作出不等式组对应的平面区域如图:(阴影部分ABC).
解:作出不等式组对应的平面区域如图:(阴影部分ABC).
令k=2x-y得y=2x-k,
平移直线y=2x-k,
由图象可知当直线y=2x-k经过点A时,直线y=2x-k的截距最小,由$\left\{\begin{array}{l}{x-y-1=0}\\{x-2y+1=0}\end{array}\right.$,可得A(3,2)
此时k最大.将A(3,2)的坐标代入目标函数2×3-2=4,
即2x-y的最大值为4.
故选:D.
点评 本题主要考查线性规划的应用,利用数形结合是解决此类问题的基本方法,利用k的几何意义是解决本题的关键.

练习册系列答案
相关题目
16. 某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )
某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )
 某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )
某商场对一个月内每天的顾客人数进行统计,得到如图所示的样本茎叶图,则该样本的中位数和众数分别是( )| A. | 46,45 | B. | 45,46 | C. | 45,45 | D. | 47,45 |
11.“一支医疗救援队里的医生和护士,包括我在内,总共是13名,下面讲到人员情况,无论是否把我计算在内,都不会有任何变化,在这些医务人员中:①护士不少于医生;②男医生多于女护士;③女护士多于男护士;④至少有一位女医生.”由此推测这位说话人的性别和职务是( )
| A. | 男护士 | B. | 女护士 | C. | 男医生 | D. | 女医生 |
8.在△ABC中,角A,B,C的对边分别为a,b,c,若a=4$\sqrt{2}$,b=5,cosA=-$\frac{3}{5}$,则向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{7\sqrt{2}}{2}$ | D. | $\frac{7\sqrt{2}}{2}$ |
15.已知正△ABC内接于半径为2的圆O,点P是圆O上的一个动点,则$\overrightarrow{PA}$•$\overrightarrow{PB}$的取值范围是( )
| A. | [0,6] | B. | [-2,6] | C. | [0,2] | D. | [-2,2] |
11.计算:4cos50°-tan40°=( )
| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
12.若复数$z=\frac{-2+3i}{i},i$是虚数单位,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |