题目内容
16.如图,某几何体的三视图如图所示,则该几何体的各条棱中最长的棱和最短的棱长度之和为( )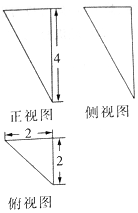
| A. | 6 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{5}$+2 | D. | 2$\sqrt{6}$+2 |
分析 本题只要画出原几何体,理清位置及数量关系,由勾股定理可得答案
解答 解:由三视图可知原几何体为三棱锥,
其中底面△ABC为俯视图中的等腰直角三角形,腰长为2,高为4,所以三棱锥的最短棱为2,最长棱为$\sqrt{(2\sqrt{2})^{2}+{4}^{2}}=2\sqrt{6}$;
故选D.
点评 本题考查了几何体的三视图,关键为几何体的还原,与垂直关系的确定.

练习册系列答案
相关题目
9.中国古代数学名著《张丘建算经》中记载:“今有马行转迟,次日减半,疾七日,行七百里其意是:现有一匹马行走的速度逐渐变慢,每天走的里数是前一天的一半,连续行走7天,共走 了 700里.若该匹马按此规律继续行走7天,则它这14天内所走的总路程为( )
| A. | $\frac{175}{32}$里 | B. | 1050 里 | C. | $\frac{22575}{32}$里 | D. | 2100里 |
11.“一支医疗救援队里的医生和护士,包括我在内,总共是13名,下面讲到人员情况,无论是否把我计算在内,都不会有任何变化,在这些医务人员中:①护士不少于医生;②男医生多于女护士;③女护士多于男护士;④至少有一位女医生.”由此推测这位说话人的性别和职务是( )
| A. | 男护士 | B. | 女护士 | C. | 男医生 | D. | 女医生 |
1.设p:2x<1,q:x(x+1)<0,则p是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
8.在△ABC中,角A,B,C的对边分别为a,b,c,若a=4$\sqrt{2}$,b=5,cosA=-$\frac{3}{5}$,则向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为( )
| A. | -$\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\frac{7\sqrt{2}}{2}$ | D. | $\frac{7\sqrt{2}}{2}$ |
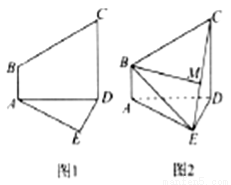
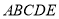 由直角梯形
由直角梯形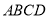 与直角△
与直角△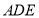 构成,如图1所示,
构成,如图1所示,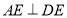 ,
,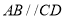 ,
,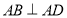 ,且
,且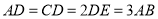 ,将梯形
,将梯形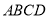 沿着
沿着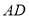 折起,形成如图2所示的几何体,且使平面
折起,形成如图2所示的几何体,且使平面
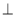 平面
平面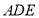 .
.
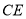 上存在点
上存在点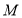 ,且
,且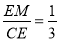 ,证明:
,证明: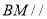 平面
平面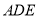 ;
;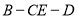 的平面角的余弦值.
的平面角的余弦值.