题目内容
3.设x,y满足约束条件$\left\{\begin{array}{l}{x≥y}\\{y≥4x-3}\\{x≥0,y≥0}\end{array}\right.$,若目标函数2z=2x+ny(n>0),z的最大值为2,则y=tan(nx+$\frac{π}{6}$)的图象向右平移$\frac{π}{6}$后的表达式为( )| A. | y=tan(2x+$\frac{π}{6}$) | B. | y=tan(x-$\frac{π}{6}$) | C. | y=tan(2x-$\frac{π}{6}$) | D. | y=tan2x |
分析 画出约束条件的可行域,利用z的最大值求出n,利用三角函数的图象变换化简求解即可.
解答 解:作出x,y满足约束条件$\left\{\begin{array}{l}{x≥y}\\{y≥4x-3}\\{x≥0,y≥0}\end{array}\right.$下的可行域,目标函数2z=2x+ny(n>0)可化为:y=$-\frac{2}{n}x$+$\frac{z}{n}$,基准线y=$-\frac{2}{n}x$,
由线性规划知识,可得当直线z=x+$\frac{n}{2}y$过点B(1,1)时,z取得最大值,即1+$\frac{n}{2}$=2,解得n=2;
则y=tan(nx+$\frac{π}{6}$)的图象向右平移$\frac{π}{6}$个单位后得到的解析式为y=tan[2(x-$\frac{π}{6}$)+$\frac{π}{6}$]=tan(2x-$\frac{π}{6}$).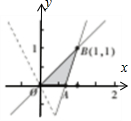
故选:C.
点评 本题考查线性规划的简单应用,三角函数的图象变换,考查转化思想以及计算能力.

练习册系列答案
相关题目
13.等比数列中{an},a1,a5为方程x2-10x+16=0的两根,则a3=( )
| A. | 4 | B. | 5 | C. | ±4 | D. | ±5 |
11.阅读如图程序框图,如果输出k=5,那么空白的判断框中应填入的条件是( )


| A. | S>-25 | B. | S<-26 | C. | S<-25 | D. | S<-24 |
18.已知i为虚数单位,a∈R,若(a+1)(a-1+i)是纯虚数,则a的值为( )
| A. | -1或1 | B. | 1 | C. | -1 | D. | 3 |
15.已知R为实数集,集合A={x|x>0},B={x|x2-x-2>0},则A∩(∁RB)=( )
| A. | (0,2] | B. | (-1,2) | C. | [-1,2] | D. | [0,4] |
12.抛物线x2=4y上一点A的纵坐标为4,则点A与抛物线焦点的距离为( )
| A. | 5 | B. | 4 | C. | $\sqrt{15}$ | D. | $\sqrt{10}$ |