题目内容
13.已知数列{an}满足a1=2,且an+1=2an+(2n-1)(n∈N*),求数列{an}的通项公式.分析 把已知的数列递推式变形,得到数列{an+1-an+2}是以5为首项,以2为公比的等比数列,写出等比数列的通项公式后结合an+1=2an+(2n-1)(n∈N*)求数列{an}的通项公式.
解答 解:由an+1=2an+2n-1,得
an+2=2an+1+2(n+1)-1,
两式作差得:an+2-an+1=2an+1-2an+2,
则$\frac{{a}_{n+2}-{a}_{n+1}+2}{{a}_{n+1}-{a}_{n}+2}$=2,
又a1=2,∴a2=5,
a2-a1+2=5.
∴数列{an+1-an+2}是以5为首项,以2为公比的等比数列,
则${a}_{n+1}-{a}_{n}+2=5•{2}^{n-1}$,
即2an+(2n-1)-an+2=5•2n-1.
∴${a}_{n}=5•{2}^{n-1}-2n-1$.
点评 本题考查了数列递推式,考查了等比关系的确定,是中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
1.设F1,F2分别为双曲线C的左右焦点,直线l过F2且与C的右支交于A,B两点,若△F1AB为直角三角形,且|F1A|,|AB|,|F1B|成等差数列,则双曲线C的离心率为( )
| A. | $\sqrt{10}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{\sqrt{10}}{3}$ | D. | $\frac{2\sqrt{10}}{5}$ |
8.一个三棱锥三视图如图所示,则该三棱锥的外接球的表面积为( )


| A. | 25π | B. | $\frac{29π}{4}$ | C. | 116π | D. | 29π |
4.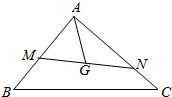 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
 如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )
如图所示,已知点G是△ABC的重心,过点G作直线与AB,AC两边分别交于M,N两点,且$\overrightarrow{AM}$=x$\overrightarrow{AB}$,$\overrightarrow{AN}$=y$\overrightarrow{AC}$,则x+2y的最小值为( )| A. | 2 | B. | $\frac{1}{3}$ | C. | $\frac{{3+2\sqrt{2}}}{3}$ | D. | $\frac{3}{4}$ |
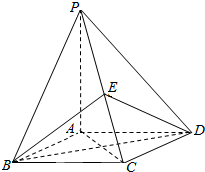 如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.
如图4,四边形ABCD为菱形,∠ABC=60°.PA⊥平面ABCD,E为PC中点.