题目内容
设f(x)是定义在R上的奇函数,且f(-1)=0,若不等式
<0对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,则不等式xf(2x)<0解集是 .
| x1f(x1)-x2f(x2) |
| x1-x2 |
考点:函数奇偶性的性质
专题:计算题,函数的性质及应用
分析:由
<0对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,知g(x)=xf(x)在(-∞,0)上单调递减,由f(x)的奇偶性可判断g(x)的奇偶性及特殊点,从而可作出草图,由图象可解g(2x)<0,进而得到答案.
| x1f(x1)-x2f(x2) |
| x1-x2 |
解答:
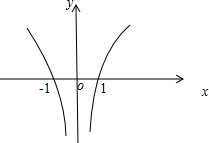 解:∵
解:∵
<0对区间(-∞,0)内任意两个不相等的实数x1,x2都成立,
∴函数g(x)=xf(x)在(-∞,0)上单调递减,
又 f(x)为奇函数,∴g(x)=xf(x)为偶函数,
g(x)在(0,+∞)上单调递增,且g(-1)=g(1)=0,
作出g(x)的草图如图所示:
xf(2x)<0即2xf(2x)<0,g(2x)<0,
由图象得,-1<2x<0或0<2x<1,解得-
<x<0或0<x
,
∴不等式xf(2x)<0解集是(-
,0)∪(0,
),
故答案为:(-
,0)∪(0,
).
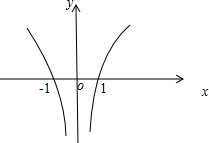 解:∵
解:∵| x1f(x1)-x2f(x2) |
| x1-x2 |
∴函数g(x)=xf(x)在(-∞,0)上单调递减,
又 f(x)为奇函数,∴g(x)=xf(x)为偶函数,
g(x)在(0,+∞)上单调递增,且g(-1)=g(1)=0,
作出g(x)的草图如图所示:
xf(2x)<0即2xf(2x)<0,g(2x)<0,
由图象得,-1<2x<0或0<2x<1,解得-
| 1 |
| 2 |
| 1 |
| 2 |
∴不等式xf(2x)<0解集是(-
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:(-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查函数的奇偶性、单调性及其应用,考查不等式的求解,综合运用函数性质化抽象不等式为具体不等式是解题关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目