题目内容
已知f(x)=2-
-x(x>-1),若f(x)≤t2-2at+1大于所有的x∈(-1,+∞),a∈[-1,1]恒成立,求实数t的取值范围.
| 1 |
| x+1 |
考点:函数恒成立问题
专题:函数的性质及应用
分析:由已知条件推导出f(x)=2-
-x的最大值为1.从而得到2ta-a2≤0对于所有的a∈[-1,1]恒成立,由此能求出实数t的取值范围.
| 1 |
| x+1 |
解答:
解:∵x>-1,∴x+1>0,
f(x)=2-
-x
=3-(
+x+1)
≤3-2
=1,
∴f(x)的最大值为1.
∴f(x)≤t2-2at+1对于所有的x∈(-1,+∞),a∈[-1,1]恒成立
等价于1≤t2-2at+1对于所有的a∈[-1,1]恒成立,
∴2ta-a2≤0对于所有的a∈[-1,1]恒成立,
令g(a)=2ta-t2,只要
,
∴t≤-2,或t≥0,或t=0.
∴实数t的取值范围是{t|t≤-2,或t≥0,或t=0}.
f(x)=2-
| 1 |
| x+1 |
=3-(
| 1 |
| x+1 |
≤3-2
|
∴f(x)的最大值为1.
∴f(x)≤t2-2at+1对于所有的x∈(-1,+∞),a∈[-1,1]恒成立
等价于1≤t2-2at+1对于所有的a∈[-1,1]恒成立,
∴2ta-a2≤0对于所有的a∈[-1,1]恒成立,
令g(a)=2ta-t2,只要
|
∴t≤-2,或t≥0,或t=0.
∴实数t的取值范围是{t|t≤-2,或t≥0,或t=0}.
点评:本题考查实数的取值范围的求法,解题时要认真审题,注意等价转化思想和均值定理的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知△ABC是边长为4的等边三角形,点D、E分别满足
=-
、
=
,则
•
=( )
| DC |
| AC |
| BE |
| EC |
| AB |
| DE |
| A、8 | B、4 | C、-8 | D、-4 |
已知等比数列{an}的前3项分别为4、6、x,则x为 ( )
| A、7 | B、8 | C、9 | D、10 |
已知平面向量
=(0,1),
=(2,1),|λ
+
|=2,则λ=( )
| a |
| b |
| a |
| b |
A、1+
| ||
B、
| ||
| C、2 | ||
| D、-1 |
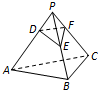 如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )
如图,正三棱锥P-ABC的所有棱长都为4.点D,E,F分别在棱PA,PB,PC上,满足DE=EF=3,DF=2的△DEF个数是( )