题目内容
9.设集合P={1,2,…,6},A,B是P的两个非空子集.则所有满足A中的最大数小于B中的最小数的集合对(A,B)的个数为:129.分析 设A中的最大数为k,其中1≤k≤n-1,整数n≥3,则A中必含元素k,另元素1,2,…,k-1,可在A中,B中必不含元素1,2,…,k;元素k+1,k+2,…,k可在B中,但不能都不在B中.由此能求出an,当n=6时,代值计算即可.
解答 解:设A中的最大数为k,其中1≤k≤n-1,整数n≥3,
则A中必含元素k,另元素1,2,…,k-1,
可在A中,故A的个数为:Ck-10+Ck-11+Ck-12+…+Ck-1k-1=2k-1,
B中必不含元素1,2,…,k,
另元素k+1,k+2,…,k可在B中,但不能都不在B中,
故B的个数为:Cn-k1+Cn-k2+…+Cn-kn-k=2n-k-1,
从而集合对(A,B)的个数为2k-1•(2n-k-1)=2n-1-2k-1,
∴an=$\sum_{n=1}^{k-1}$(2n-1-2k-1)=(n-1)•2n-1-$\frac{1-{2}^{n-1}}{1-2}$=(n-2)•2n-1+1.
当n=6时,a6=(6-2)×25+1=129
故答案为:129.
点评 本题考查排列、组合及简单计数问题,考查数列的通项公式,是中档题.

练习册系列答案
相关题目
14.抛物线y2=8x的焦点为F,其准线与x轴的交点为Q,过点F作直线与此抛物线交于A,B两点,若$\overrightarrow{FA}$•$\overrightarrow{QB}$=0,则|AF|-|BF|=( )
| A. | 8 | B. | 9 | C. | 10 | D. | 12 |
1.若命题p:?x∈R,不等式x2-2$\sqrt{2}$x+a>0恒成立,命题q:?x∈R,不等式|x-1|+|x+1|>a恒成立,则命题¬p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
 如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.
如图,平面ABCD⊥平面ABEF,四边形ABCD是矩形,四边形ABEF是等腰梯形,其中AB∥EF,AB=2AF,∠BAF=60°,O,P分别为AB,CB的中点,M为△OBF的重心.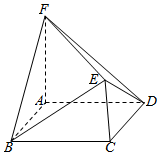 如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.
如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.