题目内容
2.设整数n≥3,集合P={1,2,…,n},A,B是P的两个非空子集.则所有满足A中的最大数小于B中的最小数的集合对(A,B)的个数为:(n-2)•2n-1+1.分析 设A中的最大数为k,其中1≤k≤n-1,整数n≥3,则A中必含元素k,另元素1,2,…,k-1,可在A中,B中必不含元素1,2,…,k;元素k+1,k+2,…,k可在B中,但不能都不在B中.由此能求出an.
解答 解:设A中的最大数为k,其中1≤k≤n-1,整数n≥3,
则A中必含元素k,另元素1,2,…,k-1,可在A中,
故A的个数为:${C}_{k-1}^{0}$+${C}_{k-1}^{1}$+…+${C}_{k-1}^{k-1}$=2k-1,
B中必不含元素1,2,…,k,
另元素k+1,k+2,…,n可在B中,但不能都不在B中,
故B的个数为:${C}_{n-k}^{1}$+${C}_{n-k}^{2}$+…+${C}_{n-k}^{n-k}$=2n-k-1,
从而集合对(A,B)的个数为2k-1•(2n-k-1)=2n-1-2k-1,
∴an=$\sum_{k=1}^{n-1}$(2n-1-2k-1)
=(n-1)•2n-1-$\frac{1-{2}^{n-1}}{1-2}$
=(n-2)•2n-1+1.
故答案为:(n-2)•2n-1+1.
点评 本题考查数列的第3项的求法,考查数列的通项公式的求法,是中档题,解题时要认真审题,注意分类讨论思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知全集U=R,集合A={x|y=log2(x-1)},B={y|y=2x},则B∩(∁UA)为( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,1] | D. | (1,2) |
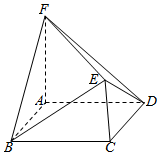 如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.
如图所示的多面体EF-ABCD中,AF⊥底面ABCD,AF∥CE,四边形ABCD为正方形,AF=2AB=2CE.