题目内容
7．已知x，y满足约束条件$\left\{\begin{array}{l}x-y+5≥0\\ x≤2\\ x+y≥0\end{array}\right.$，则z=x+2y的最小值为（ ）| A． | -3 | B． | $-\frac{5}{2}$ | C． | -2 | D． | $\frac{5}{2}$ |
分析 作出平面区域，求出角点的坐标，平移直线2x+y=0确定最小值．
解答 
解：画出满足条件的平面区域，如图示：
，
由$\left\{\begin{array}{l}{x=2}\\{y=-x}\end{array}\right.$，解得A（2，-2），
由z=x+2y得：y=-$\frac{1}{2}$x+$\frac{z}{2}$，
结合图象得直线过A（2，-2）时，z最小，最小值是-2，
故选：C．
点评 本题主要考查线性规划中的最值问题，属于基础题．
练习册系列答案
相关题目
15．
如图是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤$\frac{π}{2}}$）图象的一部分，为了得到这个函数的图象，只要将y=sinx的图象上所有的点（ ）
如图是函数y=Asin（ωx+φ）（A＞0，ω＞0，|φ|≤$\frac{π}{2}}$）图象的一部分，为了得到这个函数的图象，只要将y=sinx的图象上所有的点（ ）| A． | 向左平移$\frac{π}{8}$个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变 | |
| B． | 向右平移$\frac{π}{8}$个单位长度，再把所得各点的横坐标缩短到原来的$\frac{1}{2}$，纵坐标不变 | |
| C． | 向左平移$\frac{π}{4}$个单位长度，再把所得各点的横坐标缩短到原来的$\frac{1}{2}$，纵坐标不变 | |
| D． | 向右平移$\frac{π}{4}$个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变 |
12．已知全集U=R，集合A={x|y=log2（x-1）}，B={y|y=2x}，则B∩（∁UA）为（ ）
| A． | （0，+∞） | B． | [1，+∞） | C． | （0，1] | D． | （1，2） |
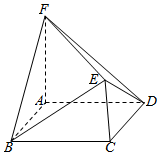如图所示的多面体EF-ABCD中，AF⊥底面ABCD，AF∥CE，四边形ABCD为正方形，AF=2AB=2CE．