题目内容
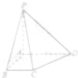如图所示，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，∠BAD=∠ABC=90°，PA=AD=2，AB=BC=1．试问在线段PA上是否存在一点M到平面PCD的距离为
| ||
| 3 |
考点：点、线、面间的距离计算
专题：空间位置关系与距离,空间角
分析：取AD中点E，连接CE，由四边形ABCE是平行四边形，平行四边形ABCE是矩形，从而△ACD是等腰直角三角形，进而CD⊥面PCA，面PCD⊥面PCA，作MF⊥PC于F，由△PMF∽△PCA，能求出PM．
解答：
解：存在M，取AD中点E，连接CE，
∵AD=2，AC=1，E是AD中点，∴BC
AE，
∴四边形ABCE是平行四边形，∵∠BAD=90°，
∴平行四边形ABCE是矩形，
∴CE⊥AD，∵AE=ED，∴CA=CD，
∵CE=AE=ED=1，AC=CD=
，PC=
，
∴△ACD是等腰直角三角形，
∴AC⊥CD，∵PA⊥面ABCD，∴PA⊥CD，∴CD⊥面PCA，
∵CD在面PCD内，∴面PCD⊥面PCA，
∵面PCD∩面PCA=PC，∴作MF⊥PC于F，
∴MF⊥面PCD，MF=
，
∵△PMF∽△PCA，∴
=
，
∴
=
，解得PM=
．
∵AD=2，AC=1，E是AD中点，∴BC| ∥ |
. |
∴四边形ABCE是平行四边形，∵∠BAD=90°，
∴平行四边形ABCE是矩形，
∴CE⊥AD，∵AE=ED，∴CA=CD，
∵CE=AE=ED=1，AC=CD=
| 2 |
| 3 |
∴△ACD是等腰直角三角形，
∴AC⊥CD，∵PA⊥面ABCD，∴PA⊥CD，∴CD⊥面PCA，
∵CD在面PCD内，∴面PCD⊥面PCA，
∵面PCD∩面PCA=PC，∴作MF⊥PC于F，
∴MF⊥面PCD，MF=
| ||
| 3 |
∵△PMF∽△PCA，∴
| MF |
| AC |
| PM |
| PC |
∴
| ||||
|
| PM | ||
|
| ||
| 2 |
点评：本题考查满足条件的点的位置的确定、平面与平面垂直的性质定理、勾股定理、二面角的求解等基础知识，意在考查方程思想、等价转化思想等数学思想方法和考生的空间想象能力、逻辑推理能力和运算求解能力．
练习册系列答案
阅读快车系列答案
相关题目
在棱长为2的正方体ABCD-A1B1C1D1中，正方形BCC1B1所在平面内的动点P到直线D1C1DC的距离之和为2
，∠CPC1=60°，则点P到直线CC1的距离为（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知F1，F2是椭圆和双曲线的公共焦点，P是它们的一个公共点，且∠F1PF2=
，则椭圆和双曲线的离心率的倒数之和的最大值为（ ）
| π |
| 3 |
| A、3 | ||||
B、
| ||||
| C、2 | ||||
D、
|