题目内容
12.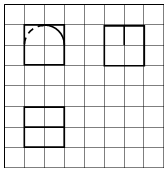 如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某几何体的三视图(其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧),则该几何体的体积为( )
如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某几何体的三视图(其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧),则该几何体的体积为( )| A. | $6+\frac{π}{4}$ | B. | $6+\frac{π}{2}$ | C. | $6-\frac{π}{4}$ | D. | $6-\frac{π}{2}$ |
分析 几何体为一个长方体,两个小正方体和两个$\frac{1}{4}$圆柱的组合体.
解答 解:由三视图可知几何体下部分为长方体,上部分为交错放置的两个小正方体和两个$\frac{1}{4}$圆柱.
长方体的棱长分别为2,2,1,小正方体的棱长为1,圆柱体的底面半径为1,高为1.
故几何体的体积V=2×2×1+2×13+$\frac{1}{4}π×{1}^{2}×1×2$=6+$\frac{π}{2}$.
故选B.
点评 本题考查了常见几何体的三视图和结构特征,体积计算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.某几何体的三视图如图所示,则其表面积为( )
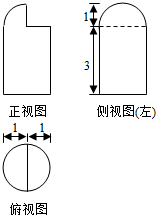

| A. | $\frac{17π}{2}$ | B. | 9π | C. | $\frac{19π}{2}$ | D. | 10π |