题目内容
2．已知函数f（x）的导函数f′（x）=a（x-1）（x-a），若f（x）在x=a处取得极大值，则实数a的取值范围是（0，1）．分析 由已知得f′（x）=a（x-1）（x-a），求出极值点，由f（x）在x=a处取得极大值，推出关系式，由此能求出实数a的取值范围．
解答 解：∵函数f（x）的导函数f′（x）=a（x-1）（x-a），f′（x）=0，
可得a（x-1）（x-a）=0，得：x=1，或x=a，
f（x）在x=a处取得极大值，
∴1＞a＞0，
∴实数a的取值范围为（0，1）．
故答案为：（0，1）
点评 本题考查实数的取值范围的求法，是中档题，解题时要认真审题，注意导数性质的合理运用．
练习册系列答案
相关题目
如图，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，直线F是右准线且准线方程为x=4．A、B分别是其左右顶点，P是椭圆上异于左右顶点的任意一点．直线PA、PB与椭圆的右准线分别交于E、F两点，连接AF与椭圆交于点M．
11．设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1，F2，离心率为e，过F2的直线与椭圆的交于A，B两点，若△F1AB是以A为顶点的等腰直角三角形，则e2=（ ）
| A． | 3-2$\sqrt{2}$ | B． | 5-3$\sqrt{2}$ | C． | 9-6$\sqrt{2}$ | D． | 6-4$\sqrt{2}$ |
12．
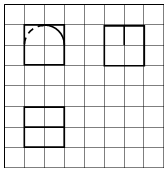如图所示，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某几何体的三视图（其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧），则该几何体的体积为（ ）
如图所示，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某几何体的三视图（其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧），则该几何体的体积为（ ）| A． | $6+\frac{π}{4}$ | B． | $6+\frac{π}{2}$ | C． | $6-\frac{π}{4}$ | D． | $6-\frac{π}{2}$ |