题目内容
3．某几何体的三视图如图所示，则其表面积为（ ）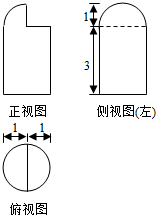
| A． | $\frac{17π}{2}$ | B． | 9π | C． | $\frac{19π}{2}$ | D． | 10π |
分析 几何体为圆柱与$\frac{1}{4}$球的组合体．表面共有5部分组成．
解答 解：由三视图可知几何体为圆柱与$\frac{1}{4}$球的组合体．
圆柱的底面半径为1，高为3，球的半径为1．
所以几何体的表面积为π×12+2π×1×3+$4π×{1}^{2}×\frac{1}{4}$+$\frac{1}{2}π×{1}^{2}$+$\frac{1}{2}π×{1}^{2}$=9π．
故选B．
点评 本题考查了圆柱与球的三视图，结构特征和面积计算，属于基础题．
练习册系列答案
相关题目
11．设椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的左、右焦点分别为F1，F2，离心率为e，过F2的直线与椭圆的交于A，B两点，若△F1AB是以A为顶点的等腰直角三角形，则e2=（ ）
| A． | 3-2$\sqrt{2}$ | B． | 5-3$\sqrt{2}$ | C． | 9-6$\sqrt{2}$ | D． | 6-4$\sqrt{2}$ |
如图，多面体SABCD中面ABCD为矩形，SD⊥AD，且SD⊥AB，AD=a（a＞0），AB=2AD，SD=$\sqrt{3}$AD．
8．已知$α∈（\frac{π}{2}，π）$，且sin（π+α）=-$\frac{3}{5}$，则tanα=（ ）
| A． | $-\frac{3}{4}$ | B． | $\frac{4}{3}$ | C． | $\frac{3}{4}$ | D． | $-\frac{4}{3}$ |
15．倾斜角为60°的直线l过抛物线y2=4x的焦点F，且与抛物线位于x轴上的部分相交于A，则△OFA的面积为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{2\sqrt{3}}}{3}$ | C． | $\sqrt{3}$ | D． | $2\sqrt{3}$ |
12．
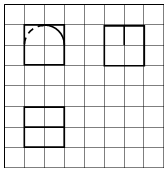如图所示，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某几何体的三视图（其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧），则该几何体的体积为（ ）
如图所示，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某几何体的三视图（其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧），则该几何体的体积为（ ）| A． | $6+\frac{π}{4}$ | B． | $6+\frac{π}{2}$ | C． | $6-\frac{π}{4}$ | D． | $6-\frac{π}{2}$ |