题目内容
4.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{6}}{3}$,右焦点为($\sqrt{2}$,0).(1)求椭圆C的方程;
(2)若过原点O作两条互相垂直的射线,与椭圆交于A,B两点,求证:点O到直线AB的距离为定值;
(3)在(2)的条件下,求△OAB面积的最大值.
分析 (1)根据焦点和离心率列方程解出a,b,c;
(2)对于AB有无斜率进行讨论,设出A,B坐标和直线方程,利用根与系数的关系和距离公式计算;
(3)求出原点到直线AB的距离最大值即可.
解答 解:(1)∵c=$\sqrt{2}$,e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$,∴a=$\sqrt{3}$,
∵a2-b2=c2,∴b=1.
∴椭圆C的方程为$\frac{{x}^{2}}{3}+{y}^{2}=1$.
(2)设A(x1,y1),B(x2,y2),
若直线斜率k存在,则设直线AB:y=kx+m.
由$\left\{\begin{array}{l}{y=kx+m}\\{{x}^{2}+3{y}^{2}=3}\end{array}\right.$,得(1+3k2)x2+6kmx+3m2-3=0.
∴$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=-\frac{6km}{1+3{k}^{2}}}\\{{x}_{1}{x}_{2}=\frac{3{m}^{2}-3}{1+3{k}^{2}}}\end{array}\right.$,
∵OA⊥OB,∴x1x2+y1y2=0.
即x1x2+(k x1+m) (k x2+m)=(1+k2) x1x2+k m(x1+x2)=0.
∴4 m2=3 k2+3
∴原点到直线AB的距离d=$\frac{|m|}{\sqrt{{k}^{2}+1}}=\frac{\sqrt{3}}{2}$.
若AB的斜率不存在时,|x1|=|y1|,可得|x1|=$\frac{\sqrt{3}}{2}$.
所以点O到直线AB的距离为定值$\frac{\sqrt{3}}{2}$.
(3)|AB|2=(1+k2)(x1-x2)2=(1+k2)[($\frac{6km}{1+3{k}^{2}}$)2-4×$\frac{3{m}^{2}-3}{1+3{k}^{2}}$]
=$\frac{3(9{k}^{4}+10{k}^{2}+1)}{9{k}^{4}+6{k}^{2}+1}$=3+$\frac{12{k}^{2}}{9{k}^{4}+6{k}^{2}+1}$=3+$\frac{12}{9{k}^{2}+6+\frac{1}{{k}^{2}}}$≤4.
当且仅当9k2=$\frac{1}{{k}^{2}}$,即k=±$\frac{\sqrt{3}}{3}$时等号成立.∴|AB|≤2.
当斜率不存在时,经检验|AB|<2.
所以S△AOB≤$\frac{1}{2}×2×\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$.
综上:△OAB面积的最大值为$\frac{\sqrt{3}}{2}$.
点评 本题考查了椭圆的性质,直线与圆锥曲线的位置关系,分类讨论思想,对于这类题目要掌握解题方法.设而不求,套用公式解决.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{2\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $2\sqrt{3}$ |
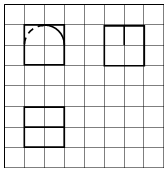 如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某几何体的三视图(其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧),则该几何体的体积为( )
如图所示,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某几何体的三视图(其中虚线弧与实线弧都是以正视图正方形中心为圆心的四分之一圆弧),则该几何体的体积为( )| A. | $6+\frac{π}{4}$ | B. | $6+\frac{π}{2}$ | C. | $6-\frac{π}{4}$ | D. | $6-\frac{π}{2}$ |
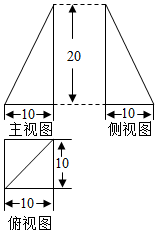 董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.
董师傅用铁皮制作一封闭的工件,且三视图如图所示(单位:cm),图中水平线与竖直线垂直),则制作该工件用去的铁皮的面积为(制作过程铁皮的损耗忽略不计)(100(3+$\sqrt{5}$)cm2.