题目内容
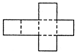 如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形内,按虚线折成正方体,则所得正方体相对面上两个数的和都相等的概率是( )
如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形内,按虚线折成正方体,则所得正方体相对面上两个数的和都相等的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:等可能事件的概率
专题:计算题
分析:先将6个数字在图中6个位置全排列,由排列数公式可得其情况数目,结合等差数列的性质分析可得,要使正方体相对面上两个数的和都相等,必须是1、6相对,2、5相对,3、4相对;由组合数公式分析可得正方体两个对面上两数字和相等的组合方式,由等可能事件的概率公式计算可得答案.
解答:
解:由题意,图中有6个位置,将1、2、3、4、5、6,这6个数字在6个位置全排列,共有A66种结果,
要使正方体相对面上两个数的和都相等,必须是1、6相对,2、5相对,3、4相对;
正方体有6个面,写第一个数字时有6种选择,
剩下四个面,则第三个数字只有4种选择,
此时剩余两个面,2个数字,有2种选择;
以此类推,可得出正方体两个对面上两数字和相等的组合方式有6×4×2=48.
要求的概率是
=
故选B.
要使正方体相对面上两个数的和都相等,必须是1、6相对,2、5相对,3、4相对;
正方体有6个面,写第一个数字时有6种选择,
剩下四个面,则第三个数字只有4种选择,
此时剩余两个面,2个数字,有2种选择;
以此类推,可得出正方体两个对面上两数字和相等的组合方式有6×4×2=48.
要求的概率是
| 48 | ||
|
| 1 |
| 15 |
故选B.
点评:本题考查等可能事件的概率计算,解题时要结合正方体的几何结构来分析,注意利用等差数列的性质进行分析.

练习册系列答案
相关题目
设函数f(x)=
sin2ωx+cos2ωx,其中0<ω<2.
(1)若f(x)的周期为π,求f(x)的单调增区间;
(2)若函数f(x)的图象的一条对称轴为x=
,求f(x)在x∈[0,π]的值域.
| ||
| 2 |
(1)若f(x)的周期为π,求f(x)的单调增区间;
(2)若函数f(x)的图象的一条对称轴为x=
| π |
| 3 |
若平面区域上的点(x,y)满足不等式
+
≤1.则该平面区域的面积是( )
|
|
| A、30 | B、40 | C、50 | D、60 |
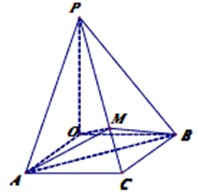 如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=
如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=