题目内容
已知复数
，(其中
为虚数单位)
（1）当复数
是纯虚数时，求实数
的值；
（2）若复数对应的点在第三象限，求实数的取值范围.
，(其中为虚数单位)（1）当复数
是纯虚数时，求实数的值；（2）若复数
对应的点在第三象限，求实数的取值范围.（1）
,（2）
,（2）试题分析：（1）根据纯虚数的概念实部为零，虚部不为零有
，解得
，即时，复数
为纯虚数.（2）因为复数对应的点在第三象限，所以实部小于零且虚部也小于零，即
，解得
，所以当时，复数对应的点在第三象限.试题解析：解：（1）由题意有
时， 解得
， 5分即
时，复数为纯虚数. 7分（2）由题意有：
，解得：
， 12分所以当
时，复数对应的点在第三象限 14分
练习册系列答案
新课标同步训练系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
，是否存在不小于2的正整数
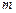，使得对于任意的正整数
都能被
、
，定义
，其中
是
、
、
，有如下四个命题：
；
；
；
.
，
，
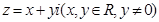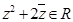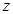在复平面上所对应点在直线
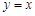上，则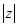
= 。
，
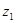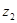对应的向量分别是
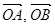，则复数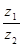
对应的点位于第 象限．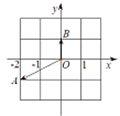
，那么z等于（ ）
