题目内容
对任意复数
、
，定义
，其中
是的共轭复数.对任意复数
、
、
，有如下四个命题：
①
；
②
；
③
；
④
.
则真命题的个数是（ ）
、，定义，其中是的共轭复数.对任意复数、、，有如下四个命题：①
；②
；③
；④
.则真命题的个数是（ ）
A． | B． | C． | D． |
B
试题分析：由定义知
=
，
=
=，故①正确；因为
=
=
，
=
=，故②正确；因为
=
=
=
，
=
=
=
，故③错误；因为
=
，，
=
，故④错，故真命题个数为2，故选B.
练习册系列答案
相关题目
.
；
为
的一个极值点，证明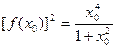
.
，(其中
为虚数单位)
是纯虚数时，求实数
的值；
是虚数单位，若复数
是纯虚数，则实数
等于
.
是虚数单位，
表示复数
的共轭复数.若
则
（ ）
