题目内容
已知数列{an}是正数组成的数列,其前n项和为Sn,对于一切n∈N*均有an与2的等差中项等于Sn与2的等比中项.
(1)计算a1,a2,a3,并由此猜想{an}的通项公式an;(2)用数学归纳法证明(1)中你的猜想.
(1)计算a1,a2,a3,并由此猜想{an}的通项公式an;(2)用数学归纳法证明(1)中你的猜想.
(1)由
=
得Sn=
可求得a1=2,a2=6,a3=10,…(5分)
由此猜想{an}的通项公式an=4n-2(n∈N+).…(7分)
(2)证明:①当n=1时,a1=2,等式成立;…(9分)
②假设当n=k时,等式成立,即ak=4k-2,…(11分)
∴ak+1=Sk+1-Sk=
-
∴(ak+1+ak)(ak+1-ak-4)=0,又ak+1+ak≠0
∴ak+1-ak-4=0,
∴ak+1=ak+4=4k-2+4=4(k+1)-2
∴当n=k+1时,等式也成立.…(13分)
由①②可得an=4n-2(n∈N+)成立.…(15分)
| an+2 |
| 2 |
| 2Sn |
| (an+2)2 |
| 8 |
由此猜想{an}的通项公式an=4n-2(n∈N+).…(7分)
(2)证明:①当n=1时,a1=2,等式成立;…(9分)
②假设当n=k时,等式成立,即ak=4k-2,…(11分)
∴ak+1=Sk+1-Sk=
| (ak+1+2)2 |
| 8 |
| (ak+2)2 |
| 8 |
∴(ak+1+ak)(ak+1-ak-4)=0,又ak+1+ak≠0
∴ak+1-ak-4=0,
∴ak+1=ak+4=4k-2+4=4(k+1)-2
∴当n=k+1时,等式也成立.…(13分)
由①②可得an=4n-2(n∈N+)成立.…(15分)

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
 ,(其中
,(其中 为虚数单位)
为虚数单位) 是纯虚数时,求实数
是纯虚数时,求实数 的值;
的值; 满足:
满足: (
( 是虚数单位),则复数
是虚数单位),则复数 ,对任意
,对任意 均满足
均满足 ,当且仅当
,当且仅当 时等号成立。
时等号成立。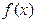 ∈M,试比较
∈M,试比较 与
与 大小.
大小. ,
, ,
, 。求证
。求证 中至少有一个不小于0。
中至少有一个不小于0。