题目内容
如果直线y-1=k（x-2）与圆x2+y2=1在第四象限内的部分有公共点，则实数k的取值范围为 ．
考点：直线与圆相交的性质
专题：计算题,直线与圆
分析：求出直线恒过的定点P，求出直线经过点A（0，-1），以及直线与圆相切时的k，根据条件，即可得到所求k的范围．
解答：
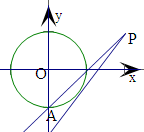解：由于直线恒过定点P（2，1），
则直线绕着定点P旋转，
当直线经过点A（0，-1），有k=
=1，
当直线与圆相切时，d=r即有
=1，
解得，k=0或
．
则由于直线和圆在第四象限内的部分有公共点时，
即有k的取值范围为（1，
]．
故答案为：（1，
]．
解：由于直线恒过定点P（2，1），则直线绕着定点P旋转，
当直线经过点A（0，-1），有k=
| -1-1 |
| 0-2 |
当直线与圆相切时，d=r即有
| |1-2k| | ||
|
解得，k=0或
| 4 |
| 3 |
则由于直线和圆在第四象限内的部分有公共点时，
即有k的取值范围为（1，
| 4 |
| 3 |
故答案为：（1，
| 4 |
| 3 |
点评：本题考查直线和圆的位置关系，考查直线和圆相交、相切的条件，考查点到直线的距离的公式的运用，考查运算能力，属于中档题．
练习册系列答案
一线名师提优试卷系列答案
相关题目
命题P：给出7个不同的实数，其中必存在2个整数x，y，满足0≤
＜
命题q：若x＞1，n≥2，n∈N，那么
-1＜
，则下列结论正确的是（ ）
| x-y |
| 1+xy |
| ||
| 3 |
| n | x |
| x-1 |
| n |
| A、（￢p）∨q是假命题 |
| B、（p￢）∧q是真命题 |
| C、p∨（q￢）是假命题 |
| D、p∧q是真命题 |
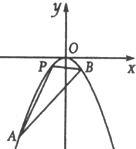已知直线l：y=kx-2与抛物线 C：x2=-2py（p＞0）交于A、B两点，O为坐标原点