题目内容
已知圆x2+y2-4x+2y+c=0与y轴相交于AB两点,圆心为P,PA⊥PB,则实数c的值是 .
考点:圆的一般方程
专题:计算题,直线与圆
分析:求出圆的圆心和半径r,由于PA⊥PB,则P到y轴的距离为
r,得到c的方程,解方程即可得到c.
| ||
| 2 |
解答:
解:圆x2+y2-4x+2y+c=0的圆心P为(2,-1),
半径为r=
,
由于PA⊥PB,则P到y轴的距离为
r,
即有2=
r=
•
,
解得,c=-3.
故答案为:-3.
半径为r=
| 5-c |
由于PA⊥PB,则P到y轴的距离为
| ||
| 2 |
即有2=
| ||
| 2 |
| ||
| 2 |
| 5-c |
解得,c=-3.
故答案为:-3.
点评:本题考查直线和圆的位置关系,考查圆的方程和运用,考查运算能力,属于基础题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
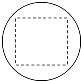 已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )
已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )| A、4π | B、8π |
| C、12π | D、16π |
设椭圆
+
=1的左右焦点分别为F1,F2,P是椭圆上的一动点,若△PF1F2是直角三角形,则△PF1F2的面积为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、3 | ||
B、3或
| ||
C、
| ||
| D、6或3 |