题目内容
命题P:给出7个不同的实数,其中必存在2个整数x,y,满足0≤
<
命题q:若x>1,n≥2,n∈N,那么
-1<
,则下列结论正确的是( )
| x-y |
| 1+xy |
| ||
| 3 |
| n | x |
| x-1 |
| n |
| A、(¬p)∨q是假命题 |
| B、(p¬)∧q是真命题 |
| C、p∨(q¬)是假命题 |
| D、p∧q是真命题 |
考点:复合命题的真假
专题:简易逻辑
分析:对于命题P:令xi为
的余数,取其中6个数,若把[0,2π)平均分成6个区间,其区间长度=
,剩下的第7个数与所在的其中的一个区间长度≤
,必然满足
0≤tan(xi-xj)<
,若取其中6个数,不能够把[0,2π)平均分成6个区间,显然成立.
对于命题q:利用(
)n-1=(
-1)[(
)n-1+(
)n-2+…+
+1]>(n+1)•(
-1),即可判断出.
| ai |
| 2kπ |
| π |
| 3 |
| π |
| 6 |
0≤tan(xi-xj)<
| ||
| 3 |
对于命题q:利用(
| n | x |
| n | x |
| n | x |
| n | x |
| n | x |
| n | x |
解答:
解:命题P:给出7个不同的实数为ai(i=1,2,…,7),令xi为
的余数(假设不等于
或
)取其中6个数,若把[0,2π)平均分成6个区间,其区间长度=
,剩下的第7个数与所在的其中的一个区间必然满足0≤tan(xi-xj)<
,若取其中6个数,不能够把[0,2π)平均分成6个区间,显然成立.
综上可得,命题P成立.其中必存在2个整数x,y,满足0≤
<
.
命题q:若x>1,n≥2,n∈N,则(
)n-1=(
-1)[(
)n-1+(
)n-2+…+
+1]>(n+1)•(
-1),化为
-1<
<
,因此正确.
综上可得:p与q都是真命题.
故选:D.
| ai |
| 2kπ |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 3 |
| ||
| 3 |
综上可得,命题P成立.其中必存在2个整数x,y,满足0≤
| x-y |
| 1+xy |
| ||
| 3 |
命题q:若x>1,n≥2,n∈N,则(
| n | x |
| n | x |
| n | x |
| n | x |
| n | x |
| n | x |
| n | x |
| x-1 |
| n+1 |
| x-1 |
| n |
综上可得:p与q都是真命题.
故选:D.
点评:本题考查了“抽屉原理”的应用、乘法公式的应用、简易逻辑的判定,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
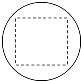 已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )
已知某一多面体内接于球构成一个组合体,如果该组合体的正视图,侧视图,俯视图均如图所示,且图中的四边形是边长为2的正方形,则该球的表面积是( )| A、4π | B、8π |
| C、12π | D、16π |
设椭圆
+
=1的左右焦点分别为F1,F2,P是椭圆上的一动点,若△PF1F2是直角三角形,则△PF1F2的面积为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、3 | ||
B、3或
| ||
C、
| ||
| D、6或3 |