题目内容
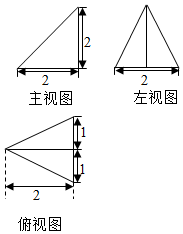
15．
已知一个几何体的三视图如图所示（单位：cm）．则该几何体的体积为8πcm3．
分析 由已知得到几何体是两个同底的圆锥的组合体，利用图中数据计算体积．
解答 
解：由已知得到几何体是底面直径为4，高为3 的两个圆锥 的组合体，所以体积为$\frac{1}{3}×π×{2}^{2}×3×2=8π$；
故答案为：8π．
点评 本题考查了由几何体的三视图求几何体的体积；关键是正确还原几何体．
练习册系列答案
相关题目
12．某高校大一新生的五名同学打算参加学校组织的“小草文学社”、“街舞俱乐部”、“足球之家”、“骑行者”四个社团．若毎个社团至少一名同学参加，每名同学至少参加一个社团且只能参加一个社团，其中同学甲不参加“街舞俱乐部”，则这五名同学不同的参加方法的种数为（ ）
| A． | 160 | B． | 180 | C． | 200 | D． | 220 |
6．有4个不同的球，四个不同的盒子，把球全部放入盒内，恰有两个盒不放球，共有（ ）种放法．
| A． | 114 | B． | 96 | C． | 84 | D． | 48 |
3．
已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得出这个几何体的内切球半径是（ ）
已知某个几何体的三视图如图所示，根据图中标出的尺寸，可得出这个几何体的内切球半径是（ ）| A． | $\frac{4}{3}$ | B． | $\frac{4}{9}$ | C． | $\sqrt{6}-2$ | D． | $3\sqrt{6}-6$ |
10．已知f（x）是定义在R上的函数，且满足①f（4）=0；②曲线y=f（x+1）关于点（-1，0）对称；③当x∈（-4，0）时f（x）=log2（$\frac{x}{{e}^{|x|}}$+ex-m+1），若y=f（x）在x∈[-4，4]上有5个零点，则实数m的取值范围为（ ）
| A． | [-3e-4，1） | B． | [-3e-4，1）∪{-e-2} | C． | [0，1）∪{-e-2} | D． | [0，1） |
20．已知数列{an}的前n项和是Sn，则下列四个命题中，错误的是（ ）
| A． | 若数列{an}是公差为d的等差数列，则数列{$\frac{{S}_{n}}{n}$}的公差为$\frac{d}{2}$的等差数列 | |
| B． | 若数列{$\frac{{S}_{n}}{n}$}是公差为d的等差数列，则数列{an}是公差为2d的等差数列 | |
| C． | 若数列{an}是等差数列，则数列的奇数项，偶数项分别构成等差数列 | |
| D． | 若数列{an}的奇数项，偶数项分别构成公差相等的等差数列，则{an}是等差数列 |
4．已知$α∈（0，\frac{π}{2}）$，且$2cos2α=cos（α-\frac{π}{4}）$，则sin2α的值为（ ）
| A． | $\frac{1}{8}$ | B． | $-\frac{1}{8}$ | C． | $-\frac{7}{8}$ | D． | $\frac{7}{8}$ |
5．已知椭圆D：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的长轴端点与焦点分别为双曲线E的焦点与实轴端点，椭圆D与双曲线E在第一象限的交点在直线y=2x上，则椭圆D的离心率为（ ）
| A． | $\sqrt{2}$-1 | B． | $\sqrt{3}$-$\sqrt{2}$ | C． | $\frac{\sqrt{5}-1}{2}$ | D． | $\frac{3-2\sqrt{2}}{2}$ |