题目内容
15．已知函数f（x）=$\left\{\begin{array}{l}{-{x}^{2}+4x，0≤x＜4}\\{lo{g}_{2}（x-2），4≤x≤6}\end{array}\right.$，若存在x1，x2∈R，当0≤x1＜4≤x2≤6时，f（x1）=f（x2），则x1f（x2）的取值范围是[3，$\frac{256}{27}$]．分析 先求出x1的范围，再将x1f（x2）转化为x的函数，利用导数知识确定x1f（x2）的取值范围．
解答 解：∵4≤x2≤6时，f（x）=log2（x-2）∈[1，2]
∴由-x2+4x∈[1，2]得2-$\sqrt{3}$≤x1≤2-$\sqrt{2}$或2+$\sqrt{2}$≤x1≤2+$\sqrt{3}$．
∵f（x1）=-x12+4x1，f（x1）=f（x2）
∴x1f（x2）=x1f（x1）=x1（-x12+4x1）
令y=x1f（x2）=x1（-x12+4x1）
则y′=x1（-3x1+8）
∴2-$\sqrt{3}$≤x1≤2-$\sqrt{2}$或2+$\sqrt{2}$≤x1≤$\frac{8}{3}$时，函数单调递增；$\frac{8}{3}$≤x1≤2+$\sqrt{3}$时，函数单调递减
∴x1f（x2）的取值范围为[3，$\frac{256}{27}$]．
故答案为[3，$\frac{256}{27}$]．
点评 本题考查分段函数，考查导数知识的运用，正确转化是解题的关键所在．
练习册系列答案
综合自测系列答案
相关题目
6．
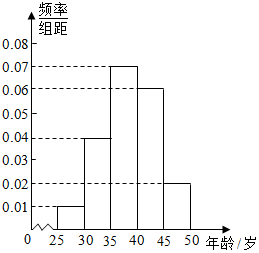某iphone手机专卖店对某市市民进行iphone手机认可度的调查，在已购买iPhone手机的1000名市民中随机抽取100名，按年龄（单位：岁）进行统计的频率分布表和频率分布直方图如下：
（1）求频数分布表中x，y的值；
（2）在抽取的这100名市民中，按年龄进行分层抽样，抽取20人参加iphone手机宣传活动，现从这20人中随机选取2人各赠送一部iphone6s手机，设这2名市民中年龄在[40，45）内的人数为X，求X的分布列及数学期望．
某iphone手机专卖店对某市市民进行iphone手机认可度的调查，在已购买iPhone手机的1000名市民中随机抽取100名，按年龄（单位：岁）进行统计的频率分布表和频率分布直方图如下：| 分组（岁） | 频数 |
| [25，30） | 5 |
| [30，35） | x |
| [35，40） | 35 |
| [40，45） | y |
| [45，50] | 10 |
| 合计 | 100 |
（2）在抽取的这100名市民中，按年龄进行分层抽样，抽取20人参加iphone手机宣传活动，现从这20人中随机选取2人各赠送一部iphone6s手机，设这2名市民中年龄在[40，45）内的人数为X，求X的分布列及数学期望．
20．已知ω＞0，函数f（x）=sin（ωx+$\frac{5π}{6}$）的一条对称轴为直线x=$\frac{π}{3}$，一个对称中心是（$\frac{π}{12}$，0），则ω有（ ）
| A． | 最小值2 | B． | 最大值2 | C． | 最小值1 | D． | 最大值1 |
4．M={x|5-x≥$\sqrt{2（x-1）}$}，N={x|x2-ax≤x-a}，当M?N时，a的取值范围是（ ）
| A． | a≥3 | B． | a≤3 | C． | a＜3 | D． | a＞3 |