题目内容
已知M={m|
∈Z},N={x|
∈N},则M∩N= .
| m-4 |
| 2 |
| x+3 |
| 2 |
考点:交集及其运算
专题:集合
分析:由已知的集合整理变形可得M为偶数集,N为奇数集的子集,则M∩N可求.
解答:
解:由
∈Z,得m=2k+4,k∈Z.
M={m|
∈Z}={m|m=2k+4,k∈Z}={m|m=2(k+2),k∈Z},
由
∈N,得x=2l-3,l∈N.
N={x|
∈N}={x|x=2l-3,l∈N}={x|x=2(l-1)-1,l∈N}.
∴M∩N=∅.
故答案为:∅.
| m-4 |
| 2 |
M={m|
| m-4 |
| 2 |
由
| x+3 |
| 2 |
N={x|
| x+3 |
| 2 |
∴M∩N=∅.
故答案为:∅.
点评:本题考查了交集及其运算,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目
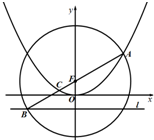 如图,已知点F是抛物线x2=4y的焦点,直线l为准线,点A是抛物线上一点.以F点为圆心,|AF|为半径作圆M交抛物线的准线l于点B.若A,B,F三点共线,则|AC|=( )
如图,已知点F是抛物线x2=4y的焦点,直线l为准线,点A是抛物线上一点.以F点为圆心,|AF|为半径作圆M交抛物线的准线l于点B.若A,B,F三点共线,则|AC|=( )A、
| ||
| B、16 | ||
C、
| ||
| D、8 |
在等差数列{an}中,已知a5+a7=16,则该数列前11项和S11的值是( )
| A、88 | B、58 |
| C、143 | D、176 |
已知集合A={x|-3≤x≤1},B={x|x≤2},则集合A∪B( )
| A、{x|-3≤x≤1} |
| B、{x|-3≤x≤2} |
| C、{x|x<1} |
| D、{x|x≤2} |