题目内容

15．已知四面体A-BCD中，△ABC和△BCD都是边长为6的正三角形，则当四面体的体积最大时，其外接球的表面积是（　　）
A．60πB．30πC．20πD．15π

分析 当四面体的体积最大时，平面ABC⊥平面BCD，取AD，BC中点分别为E，F，连接EF，AF，DF，求出EF，判断三棱锥的外接球球心O在线段EF上，连接OA，OC，求出半径，然后求解三棱锥的外接球的表面积．

解答 解：当四面体的体积最大时，平面ABC⊥平面BCD，
取AD，BC中点分别为E，F，连接EF，AF，DF，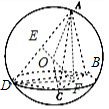
由题意知AF⊥DF，AF=CF=3$\sqrt{3}$，
∴EF=$\frac{1}{2}$AD=$\frac{3\sqrt{6}}{2}$，
易知三棱锥的外接球球心O在线段EF上，
连接OA，OC，有R2=AE2+OE2，R2=DF2+OF2，
∴R2=（$\frac{3\sqrt{6}}{2}$）2+OE2，R2=32+（$\frac{3\sqrt{6}}{2}$-OE）2，
∴R=$\sqrt{15}$，
∴三棱锥的外接球的表面积为4πR2=60π．
故选A．

点评 本小题主要考查球的内接几何体的相关计算问题，对考生的空间想象能力与运算求解能力以及数形结合思想都提出很高要求，本题是一道综合题．

练习册系列答案
相关题目
5．已知定义在（0，+∞）上的单调函数f（x），对?x∈（0，+∞），都有f[f（x）-lnx]=e+1，则函数g（x）=f（x）-f′（x）-e的零点所在区间是（　　）
A．（1，2）B．（2，3）C．（$\frac{1}{2}$，1）D．（0，$\frac{1}{2}$）
6．已知点P（0，-2），点A，B分别为椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左右顶点，直线BP交E于点Q，△ABP是等腰直角三角形，且$\overrightarrow{PQ}$=$\frac{3}{2}\overrightarrow{QB}$．
（1）求E的方程；
（2）设过点的动直线l与E相交于M，N两点，当坐标原点O位于MN以为直径的圆外时，求直线l斜率的取值范围．
3．已知球O的半径为R，A，B，C三点在球O的球面上，球心O到平面ABC的距离为$\frac{\sqrt{3}}{2}$R，AB=AC=BC=2$\sqrt{3}$，则球O的表面积为（　　）
A．$\frac{16}{3}$πB．16πC．$\frac{64}{3}$πD．64π
10．已知袋子中放有大小和形状相同的小球若干，其中标号为0的小球1个，标号为1的小球1个，标号为2的小球n个．若从袋子中随机抽取1个小球，取到标号为2的小球的概率是$\frac{1}{2}$．
（1）求n的值；
（2）从袋子中不放回地随机抽取2个小球，记第一次取出的小球标号为a，第二次取出的小球标号为b．
（i）记“a+b=2”为事件A，求事件A的概率；
（ii）在区间[0，2]内任取2个实数x，y，求事件“x2+y2＞（a-b）2恒成立”的概率．
20．已知某几何体的三视图如图，则该几何体的表面积是（　　）
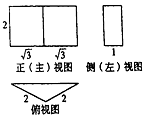
A．$4+4\sqrt{3}$B．$4+6\sqrt{3}$C．$8+6\sqrt{3}$D．$8+8\sqrt{3}$
7．已知过球面上A，B，C三点的截面和球心的距离等于球半径的一半，且AB=BC=CA=2，则球面的面积是$\frac{64π}{9}$．
4．某几何体的三视图如图所示，则它的表面积为（　　）
A．12πB．57πC．45πD．81π
5．已知正三角形ABC的三个顶点都在球心为O、半径为3的球面上，且三棱锥O-ABC的高为2，点D是线段BC的中点，过点D作球O的截面，则截面积的最小值为（　　）
A．$\frac{15π}{4}$B．4πC．$\frac{7π}{2}$D．3π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网