题目内容

14．f（x）=$\sqrt{{x}^{2}+2x+1}$，g（x）=|x-1|．
（1）求不等式|f（x）-1|＜2的解集；
（2）当|a+b|-|a-b|＞2|b|[f（x）-g（x）]（b≠0，a，b∈R）的解集非空，求x的取值范围．

分析 （1）利用绝对值的意义，分类讨论，可得结论；
（2）由题意，|x+1|＜|x-1|，即可求x的取值范围．

解答 解：（1）不等式|f（x）-1|＜2，可化为不等式||x+1|-1|＜2，即1＜|x+1|＜3，
∴-3＜x+1＜-1或1＜x+1＜3，
∴-4＜x＜-2或0＜x＜2，
∴不等式的解集为{x|-4＜x＜-2或0＜x＜2}；
（2）由题意，|x+1|＜|x-1|，∴x2+2x+1＜x2-2x+1，∴x＜0．

点评 本题考查绝对值不等式的解法，考查学生的计算能力，属于中档题．

练习册系列答案
相关题目
4．函数$f（x）={（\frac{1}{2}）^{\sqrt{x-{x^2}}}}$的单调递增区间为（　　）
A．$（-∞，\frac{1}{2}]$B．$[{0，\frac{1}{2}}]$C．$[\frac{1}{2}，+∞）$D．$[{\frac{1}{2}，1}]$
5．已知定义在（0，+∞）上的单调函数f（x），对?x∈（0，+∞），都有f[f（x）-lnx]=e+1，则函数g（x）=f（x）-f′（x）-e的零点所在区间是（　　）
A．（1，2）B．（2，3）C．（$\frac{1}{2}$，1）D．（0，$\frac{1}{2}$）
2．已知直线l与椭圆C：$\frac{x^2}{4}+{y^2}=1$交于A，B两点，且|AB|=2，则直线l与圆x2+y2=1的位置关系为（　　）
A．相离B．相交C．相切D．相交或相切
9．定义：二阶行列式$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc（a，b，c，d∈R）．已知数列{an}满足a1=1，a2=2，$|\begin{array}{l}{{a}_{n+2}}&{{a}_{n+1}}\\{{a}_{n+1}}&{{a}_{n}}\end{array}|$=（-1）n+1（n∈N*）．
（Ⅰ）求a3，a4，a5；
（Ⅱ）求证：an+2=2an+1+an（n∈N*）
（Ⅲ）试问该数列任意两个相邻项的平方和仍然是该数列中的一个项吗？如果是，请证明你的结论；如果不是，请说明理由．
19．已知某几何体的三视图如图所示，则该几何体的体积为（　　）
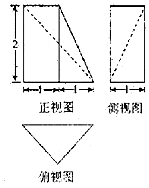
A．$\frac{2}{3}$B．$\frac{4}{3}$C．2D．$\frac{8}{3}$
6．已知点P（0，-2），点A，B分别为椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左右顶点，直线BP交E于点Q，△ABP是等腰直角三角形，且$\overrightarrow{PQ}$=$\frac{3}{2}\overrightarrow{QB}$．
（1）求E的方程；
（2）设过点的动直线l与E相交于M，N两点，当坐标原点O位于MN以为直径的圆外时，求直线l斜率的取值范围．
3．已知球O的半径为R，A，B，C三点在球O的球面上，球心O到平面ABC的距离为$\frac{\sqrt{3}}{2}$R，AB=AC=BC=2$\sqrt{3}$，则球O的表面积为（　　）
A．$\frac{16}{3}$πB．16πC．$\frac{64}{3}$πD．64π
4．某几何体的三视图如图所示，则它的表面积为（　　）
A．12πB．57πC．45πD．81π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网