题目内容
11. 如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).
如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).①该多面体是三棱锥;②平面BAD⊥平面BCD;
③平面BAC⊥平面ACD;④该多面体外接球的表面积为5πa2.
分析 利用图形翻折,结合勾股定理,确定该多面体是以A,B,C,D为顶点的三棱锥,利用线面垂直,判定面面垂直,即可得出结论.
解答 解:长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,
使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,则
①由于$(\sqrt{2}a)^{2}+(\sqrt{2}a)^{2}=4{a}^{2}$,∴该多面体是以A,B,C,D为顶点的三棱锥,正确;
②∵AP⊥BP,AP⊥CP,∴AP⊥平面BCD,∵AP?平面BAD,∴平面BAD⊥平面BCD,正确;
③与②同理,可得平面BAC⊥平面ACD,正确;
④该多面体外接球的半径为$\frac{\sqrt{5}}{2}$a,表面积为5πa2,正确.
故答案为①②③④.
点评 本题考查棱锥的结构特征,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.f(x)为奇函数,当x>0时,f(x)=π-arccos(sinx)则x<0时,f(x)=( )
| A. | arccos(sinx) | B. | π+arccos(sinx) | C. | -arccos(sinx) | D. | -π-arccos(sinx) |
2.已知直线l与椭圆C:$\frac{x^2}{4}+{y^2}=1$交于A,B两点,且|AB|=2,则直线l与圆x2+y2=1的位置关系为( )
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相交或相切 |
19.已知某几何体的三视图如图所示,则该几何体的体积为( )
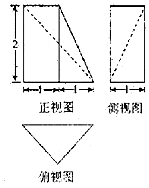

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
3.已知球O的半径为R,A,B,C三点在球O的球面上,球心O到平面ABC的距离为$\frac{\sqrt{3}}{2}$R,AB=AC=BC=2$\sqrt{3}$,则球O的表面积为( )
| A. | $\frac{16}{3}$π | B. | 16π | C. | $\frac{64}{3}$π | D. | 64π |
20.已知某几何体的三视图如图,则该几何体的表面积是( )
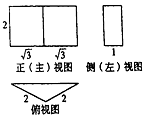

| A. | $4+4\sqrt{3}$ | B. | $4+6\sqrt{3}$ | C. | $8+6\sqrt{3}$ | D. | $8+8\sqrt{3}$ |
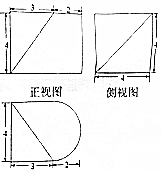 某几何体的三视图如图所示(其中俯视图中的圆弧是半圆),则该几何体的体积为32+8π.
某几何体的三视图如图所示(其中俯视图中的圆弧是半圆),则该几何体的体积为32+8π.