题目内容
12.在△ABC中,三内角A,B,C的对边分别为a,b,c.(1)若c=$\sqrt{6},A={45°}$,a=2,求C,b;
(2)若a=btanA,且B为钝角,证明:B-A=$\frac{π}{2}$,并求sinA+sinC的取值范围.
分析 (1)由正弦定理即可求出C的大小,再根据正弦定理和两角和的正弦公式即可求出b
(2)根据正弦定理、商的关系化简已知的式子,由条件和诱导公式求出B-A的值,求出C和A的范围,由诱导公式和二倍角的余弦公式变形化简,利用换元法和二次函数的性质求出式子的范围.
解答 解:(1)由正弦定理可得$\frac{c}{sinC}$=$\frac{a}{sinA}$,
∵c=$\sqrt{6},A={45°}$,a=2,
∴sinC=$\frac{\sqrt{6}×\frac{\sqrt{2}}{2}}{2}$=$\frac{\sqrt{3}}{2}$,
∴C=60°或120°,
由正弦定理可得b=$\frac{asinB}{sinA}$
当C=60°,sinB=sin(A+C)=sin45°cos60°+cos45°sin60°=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∴b=$\frac{2×\frac{\sqrt{6}+\sqrt{2}}{4}}{\frac{\sqrt{2}}{2}}$=1+$\sqrt{3}$,
当C=120°,sinB=sin(A+C)=sin45°cos120°+cos45°sin120°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
∴b=$\sqrt{3}$-1,
(2)由题意得a=btanA,
∴由正弦定理得sinA=sinB•$\frac{sinA}{cosA}$,则sinB=cosA,
∵B为钝角,∴B=$\frac{π}{2}$+A,
∴B-A=$\frac{π}{2}$;
∴C=π-(A+B)=π-(A+$\frac{π}{2}$+A)=$\frac{π}{2}$-2A>0,
∴A∈(0,$\frac{π}{4}$),
∴sinA+sinC=sinA+sin($\frac{π}{2}$-2A)
=sinA+cos2A=sinA+1-2sin2A
=-2(sinA-$\frac{1}{4}$)2+$\frac{9}{8}$,
∵A∈(0,$\frac{π}{4}$),∴0<sinA<$\frac{\sqrt{2}}{2}$,
∴由二次函数可知,$\frac{\sqrt{2}}{2}$<-2(sinA-$\frac{1}{4}$)2+$\frac{9}{8}$≤$\frac{9}{8}$,
∴sinA+sinC的取值范围为($\frac{\sqrt{2}}{2}$,$\frac{9}{8}$]
点评 本题考查三角函数中恒等变换的应用,正弦定理,以及换元法和二次函数的性质,熟练掌握公式和定理是解题的关键.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
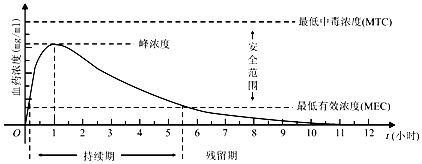
根据图中提供的信息,下列关于成人使用该药物的说法中,不正确的是( )
| A. | 首次服用该药物1单位约10分钟后,药物发挥治疗作用 | |
| B. | 每次服用该药物1单位,两次服药间隔小于2小时,一定会产生药物中毒 | |
| C. | 每间隔5.5小时服用该药物1单位,可使药物持续发挥治疗作用 | |
| D. | 首次服用该药物1单位3小时后,再次服用该药物1单位,不会发生药物中毒 |
| 日期 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 优惠金额x(千元) | 10 | 11 | 13 | 12 | 8 |
| 销售量y(辆) | 23 | 25 | 30 | 26 | 16 |
(1)若选取的是第1年与第5年的两组数据,请根据其余三年的数据,求出y关于x的线性回归方程$\hat y=\hat bx+\hat a$;
(2)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2辆,则认为得到的线性回归方程是可靠的,试问(1)中所得的线性回归方程是否可靠?
相关公式:$\hat b=\frac{{\sum_{i=1}^n{({{x_i}-\overline x})({{y_i}-\overline y})}}}{{\sum_{i=1}^n{{{({{x_i}-\overline x})}^2}}}}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\hat a=\overline y-\hat b\overline x$.
 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,无宽,高1丈.现给出该楔体的三视图,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )
《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,无宽,高1丈.现给出该楔体的三视图,其中网格纸上小正方形的边长为1丈,则该楔体的体积为( )| A. | 4立方丈 | B. | 5立方丈 | C. | 6立方丈 | D. | 8立方丈 |
| A. | (1,2) | B. | (0,1) | C. | (-1,0) | D. | (-2,-1) |
 如图,网格纸的小正方形的边长是1,粗线表示一正方体被某平面截得的几何体的三视图,则该几何体的体积为( )
如图,网格纸的小正方形的边长是1,粗线表示一正方体被某平面截得的几何体的三视图,则该几何体的体积为( )