题目内容
已知f(x)=
x2+sin(
+x),则f′(x)的大致图象是( )
| 1 |
| 4 |
| π |
| 2 |
A、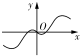 |
B、 |
C、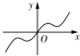 |
D、 |
考点:利用导数研究函数的单调性
专题:函数的性质及应用
分析:先化简,再求其导数,得出导函数是奇函数,排除B,D.再取x=
,得到f′(
)<0,从而排除C,即可得出正确答案.
| π |
| 6 |
| π |
| 6 |
解答:
解:∵f(x)=
x2+sin(
+x)=
x2+cosx,
∴f′(x)=
x-sinx,
设g(x)=
x-sinx,
∴g(-x)=-
x+sinx=-g(x),
∴g(x)的图象关于原点对称,即f′(x)的图象关于原点对称,排除BD
当x=
时,f′(
)=
×
-sin
=
-
=
<0,排除C,
故选:A
| 1 |
| 4 |
| π |
| 2 |
| 1 |
| 4 |
∴f′(x)=
| 1 |
| 2 |
设g(x)=
| 1 |
| 2 |
∴g(-x)=-
| 1 |
| 2 |
∴g(x)的图象关于原点对称,即f′(x)的图象关于原点对称,排除BD
当x=
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 12 |
| 1 |
| 2 |
| π-6 |
| 12 |
故选:A
点评:本题主要考查的导数运算法则,以及函数的奇偶性和利用特殊值法,属于基础题

练习册系列答案
相关题目
已知点P是平行四边形ABCD所在平面外一点,如果
=(2,-1,-4),
=(4,2,0),
=(-1,2,-1).对于结论:①AP⊥AB;②AP⊥AD;③
是平面ABCD的法向量;④
∥
.其中正确的个数是( )
| AB |
| AD |
| AP |
| AP |
| AP |
| BD |
| A、1 | B、2 | C、3 | D、4 |
已知焦点在x轴上的双曲线
-
=1的渐近线经过点P(1,
),则该双曲线的离心率是( )
| x2 |
| m |
| y2 |
| n |
| 3 |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |