Question

19．在正棱柱ABC-A₁B₁C₁中，M为△A₁B₁C₁的重心，若$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$，则$\overrightarrow{A{C}_{1}}$=$\overrightarrow{b}+\overrightarrow{c}$，$\overrightarrow{CM}$=$\overrightarrow{c}+\frac{\overrightarrow{a}}{3}-\frac{2\overrightarrow{b}}{3}$．

Answer 1

分析 利用正棱柱ABC-A₁B₁C₁的性质及空间向量加法法则直接求解．

解答 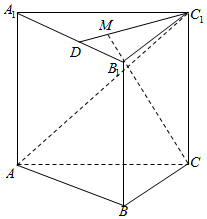解：∵在正棱柱ABC-A₁B₁C₁中，M为△A₁B₁C₁的重心，
$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$，
∴$\overrightarrow{A{C}_{1}}$=$\overrightarrow{AC}+\overrightarrow{C{C}_{1}}$=$\overrightarrow{b}+\overrightarrow{c}$，
$\overrightarrow{CM}$=$\overrightarrow{C{C}_{1}}+\overrightarrow{{C}_{1}M}$=$\overrightarrow{c}+\frac{2}{3}\overrightarrow{{C}_{1}D}$=$\overrightarrow{c}+\frac{2}{3}$×$\frac{1}{2}$（$\overrightarrow{{C}_{1}{A}_{1}}+\overrightarrow{{C}_{1}{B}_{1}}$）
=$\overrightarrow{c}+\frac{1}{3}$（-$\overrightarrow{b}$+$\overrightarrow{AB}-\overrightarrow{AC}$）
=$\overrightarrow{c}$+$\frac{1}{3}$（-$\overrightarrow{b}+\overrightarrow{a}-\overrightarrow{b}$）
=$\overrightarrow{c}+\frac{\overrightarrow{a}}{3}-\frac{2\overrightarrow{b}}{3}$．
故答案为：$\overrightarrow{b}$+$\overrightarrow{c}$，$\overrightarrow{c}+\frac{\overrightarrow{a}}{3}-\frac{2\overrightarrow{b}}{3}$．

点评 本题考查向量的求法，是基础题，解题时要认真审题，注意正棱柱ABC-A₁B₁C₁的性质及空间向量加法法则的合理运用．