题目内容

已知圆柱有一个内接长方体ABCD-A1B1C1D1，长方体的对角线长为10
2
，且圆柱的侧面展开图是面积为100π的矩形，则此圆柱体积是
 
．
考点：组合几何体的面积、体积问题
专题：空间位置关系与距离
分析：设圆柱半径为r，高为h，利用长方体的对角线的长度与棱长的关系，结合圆柱的侧面积为100π，求出圆柱的底面半径与高，即可求解圆柱的体积．
解答： 解：设圆柱半径为r，高为h
则有，4r2+h2=(10
2
)2，且2πrh=100π
4r2+h2=200且h=
50
r
即4r2+（
50
r
）2=200
即4r4 -200r2 +2500=0
即r4 -50r2 +625=0
即r2=25
r=5，h=10
体积V=πr2h=250π．
故答案为：250π．
点评：本题考查旋转体以及内接体的关系，几何体的体积的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
如图：三棱柱A1B1C1-ABC，A1A⊥AC，A1A⊥AB，AB=AC=1，A1B=2，E是A1B的中点．
（Ⅰ）若BC=
2
，求证：平面ACE⊥平面A1AB；
（Ⅱ）若∠CAB=120°，求二面角A1-AE-C的余弦值．
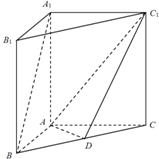直三棱柱ABC-A1B1C1中，AB⊥AC，AB=AC=1，AA1=
2
，D为BC中点．
（Ⅰ）求证：AD⊥平面BC1；
（Ⅱ）求证：A1B∥平面AC1D；
（Ⅲ）求二面角D-AC1-C的正弦值．
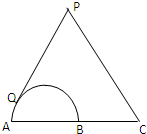如图，点C为半圆的直径AB延长线上一点，AB=BC=2，过动点P作半圆的切线PQ，若PC=
3
PQ，则△PAC的面积的最大值为
 
．
已知m∈R时，函数f（x）=m（x2-1）+x-a恒有零点，则实数a的取值范围是
 
．
已知△ABC面积S和三边a，b，c满足：S=a2-（b-c）2，b+c=8，则△ABC面积S的最大值为
 
．
若对任意x＞0，
x
x2+3x+1
≤a恒成立，则a的最小值为
 
．
一动圆P与圆O1：x2+y2=1和圆O2：x2+y2-8x+7=0均内切，则动圆P圆心的轨迹是
 
．
已知全集U={0，1，2，3，4}，集合A={1，2}，B={2，3，4}，则B∩∁UA的子集个数有（　　）
A、2B、4C、8D、16

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网