题目内容
将3名男生和4名女生排成一行,甲、乙两人必须站在两头,则不同的排列方法共有 种.(用数字作答)
考点:计数原理的应用
专题:计算题,排列组合
分析:甲、乙两人必须站在两头,有
=2种方法,其余5人站在中间,有
=120种方法,根据乘法原理可得结论.
| A | 2 2 |
| A | 5 5 |
解答:
解:甲、乙两人必须站在两头,有
=2种方法,其余5人站在中间,有
=120种方法,
根据乘法原理可得,不同的排列方法共有2×120=240种方法.
故答案为:240.
| A | 2 2 |
| A | 5 5 |
根据乘法原理可得,不同的排列方法共有2×120=240种方法.
故答案为:240.
点评:乘法原理去考虑问题;即做一件事情,完成它需要分成n个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法,…,做第n步有Mn种不同的方法,那么完成这件事就有M1×M2×…×Mn种不同的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
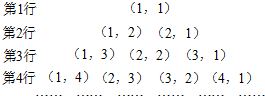 把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.
把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.