题目内容
已知△ABC的三个顶点在以O为球心的球面上,且cosA=
,BC=1,AC=3,三棱锥O-ABC的体积为
,则球O的表面积为 .
2
| ||
| 3 |
| ||
| 6 |
考点:球内接多面体,球的体积和表面积
专题:球
分析:通过A的余弦函数求出正弦函数值,求出B的大小,利用三棱锥O-ABC的体积为
,求出O到底面的距离,求出球的半径,然后求出球的表面积.
| ||
| 6 |
解答:
解:△ABC的三个顶点在以O为球心的球面上,且cosA=
,BC=1,AC=3,
∴sinA=
=
,
由正弦定理可知:
=
,
∴sinB=1,B=90°.斜边AC的中点就是△ABC的外接圆的圆心,
∵三棱锥O-ABC的体积为
,
又AB=
=2
,
∴
×
•AB•BC•h=
,
∴h=
,
∴R=
=2,
球O的表面积为4πR2=16π.
故答案为:16π.
2
| ||
| 3 |
∴sinA=
| 1-cos2A |
| 1 |
| 3 |
由正弦定理可知:
| BC |
| sinA |
| AC |
| sinB |
∴sinB=1,B=90°.斜边AC的中点就是△ABC的外接圆的圆心,
∵三棱锥O-ABC的体积为
| ||
| 6 |
又AB=
| AC2-BC2 |
| 2 |
∴
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 6 |
∴h=
| ||
| 2 |
∴R=
(
|
球O的表面积为4πR2=16π.
故答案为:16π.
点评:本题考查球的表面积的求法,球的内含体与三棱锥的关系,考查空间想象能力以及计算能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
已知当|x|<
时,有
=1-2x+4x2-…+(-2x)n+…,根据以上信息,若对任意|x|<
,都有
=a0+a1x+a2x2+…+anxn+…,则a10= .
| 1 |
| 2 |
| 1 |
| 1+2x |
| 1 |
| 2 |
| x |
| (1-x3)(1+2x) |
已知奇函数y=f(x)在区间[-b,-a]上为减函数,且在此区间上,y=f(x)的最小值为2,则函数y=|f(x)|在区间[a,b]上是( )
| A、增函数且最大值为2 |
| B、增函数且最小值为2 |
| C、减函数且最大值为2 |
| D、减函数且最小值为2 |
执行如图的程序框图,则输出的S的值为( )


| A、1 | B、2 | C、3 | D、4 |
已知f(x)=x3-3x,则函数h(x)=f[f(x)]-1的零点个数是( )
| A、3 | B、5 | C、7 | D、9 |
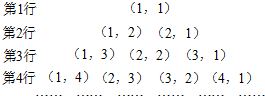 把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.
把数对(x,y)(x,y∈N+)按一定规律排列成如图所示的三角形数表,令aij表示数表中第i行第j个数对.