题目内容
设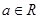 ,函数
,函数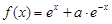 的导函数是
的导函数是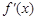 ,且
,且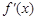 是奇函数,则
是奇函数,则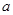 的值为( )
的值为( )
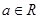 ,函数
,函数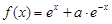 的导函数是
的导函数是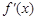 ,且
,且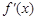 是奇函数,则
是奇函数,则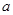 的值为( )
的值为( )A. | B. | C. | D. |
A
试题分析:∵
 ,要
,要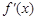 是奇函数,则
是奇函数,则 ,
,∴
 ,即
,即 ,∴
,∴ ,故选A.
,故选A.
练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
题目内容
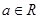 ,函数
,函数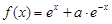 的导函数是
的导函数是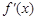 ,且
,且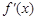 是奇函数,则
是奇函数,则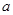 的值为( )
的值为( )A. | B. | C. | D. |
 ,要
,要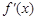 是奇函数,则
是奇函数,则 ,
, ,即
,即 ,∴
,∴ ,故选A.
,故选A.
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案