题目内容
10.若复数z=$\frac{a+i}{2i}$(a∈R,i为虚数单位)的实部与虚部相等,则z的模等于( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
分析 利用复数的运算法则、实部与虚部的定义、模的计算公式即可得出.
解答 解:复数z=$\frac{a+i}{2i}$=$\frac{-i(a+i)}{-i•2i}$=$\frac{1}{2}-\frac{1}{2}ai$的实部与虚部相等,
∴$\frac{1}{2}=-\frac{1}{2}a$,解得a=-1.
∴z=$\frac{1}{2}+\frac{1}{2}$i,
则|z|=$\sqrt{(\frac{1}{2})^{2}×2}$=$\frac{\sqrt{2}}{2}$.
故选:B.
点评 本题考查了复数的运算法则、实部与虚部的定义、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.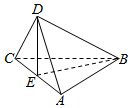 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )| A. | 直线AB⊥直线CD,且直线AC⊥直线BD | |
| B. | 直线AB⊥平面BCD,且直线AC⊥平面BDE | |
| C. | 平面ABC⊥平面BDE,且平面ACD⊥BDE | |
| D. | 平面ABD⊥平面BCD,且平面ACD⊥平面BDE |
1.幂函数y=f(x)的图象经过点(2,4),则f(x)的解析式为( )
| A. | f(x)=2x | B. | f(x)=x2 | C. | f(x)=2x | D. | f(x)=log2x+3 |
18.若m为实数且(2+mi)(m-2i)=-4-3i,则m=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
15.已知向量$\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(-3,1)则下列结论正确的是( )
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$) |