题目内容
有n粒球(n≥2,n∈N*),任意将它们分成两堆,求出两堆球的乘积,再将其中一堆任意分成两堆,求这出两堆球的乘积,如此下去,每次任意将其中一堆分成两堆,求这出两堆球的乘积,直到每堆球都不能再分为止,记所有乘积之和为Sn.例如对于4粒球有如下两种分解:
(4)→(1,3)→(1,1,2)→(1,1,1,1),此时S4=1×3+1×2+1×1=6;
(4)→(2,2)→(1,1,2)→(1,1,1,1),此时S4=2×2+1×1+1×1=6.
于是发现S4为定值,请你研究Sn的规律,归纳Sn= .
(4)→(1,3)→(1,1,2)→(1,1,1,1),此时S4=1×3+1×2+1×1=6;
(4)→(2,2)→(1,1,2)→(1,1,1,1),此时S4=2×2+1×1+1×1=6.
于是发现S4为定值,请你研究Sn的规律,归纳Sn=
考点:归纳推理
专题:新定义
分析:从n=1开始研究,到n=2,n=3,n=4,n=5,…找出Sn的共性,得到和的一般性规律,从而解决本题.
解答:
解:(2)→(1,1),此时S2=1×1=1;
(3)→(1,2)→(1,1,1),此时S3=1×2+1×1=2+1=3;
(4)→(1,3)→(1,1,2)→(1,1,1,1),此时S4=1×3+1+2+1×1=3+2+1=6;
(5)→(1,4)→(1,1,3)→(1,1,1,2)→(1,1,1,1,1),
此时S5=1×4+1×3+1×2+1×1=4+3+2+1=10;
归纳猜想:Sn=(n-1)+(n-2)+(n-3)+…+3+2+1=
×(n-1)=
.
故答案为:
.
(3)→(1,2)→(1,1,1),此时S3=1×2+1×1=2+1=3;
(4)→(1,3)→(1,1,2)→(1,1,1,1),此时S4=1×3+1+2+1×1=3+2+1=6;
(5)→(1,4)→(1,1,3)→(1,1,1,2)→(1,1,1,1,1),
此时S5=1×4+1×3+1×2+1×1=4+3+2+1=10;
归纳猜想:Sn=(n-1)+(n-2)+(n-3)+…+3+2+1=
| 1+(n-1) |
| 2 |
| n2-n |
| 2 |
故答案为:
| n2-n |
| 2 |
点评:本题考查的是归纳推理,要求学生理解本题的新定义的规律,从出发现规律,得到本题的解.另外,本题还可以尝试从S5=4+S4的角度去寻找解题规律.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=2
sinxcosx+
cos2x的最小正周期和振幅分别是( )
| 6 |
| 2 |
A、π,
| ||
B、π,
| ||
| C、2π,1 | ||
D、π,2
|
已知点O(0,0),A(1,2),B(3,2),以线段AB为直径作圆C,则直线l:x+y-3=0与圆C的位置关系是( )
| A、相交且过圆心 | B、相交但不过圆心 |
| C、相切 | D、相离 |
定义在R上的函数f(x)=e|x|+ln
,且f(x+t)>f(x)在x∈(-1,+∞)上恒成立,则关于x的方程f(2x-1)=f(t)-e的根的个数叙述正确的是( )
| x2+1 |
| A、有两个 | B、有一个 |
| C、没有 | D、上述情况都有可能 |
已知点O(0,0),A0(0,1),An(6,7),点A1,A2,…,An-1(n∈N,n≥2)是线段A0An的n等分点,则|
+
+…+
+
|等于( )
| OA0 |
| OA1 |
| OAn-1 |
| OAn |
| A、5n | B、10n |
| C、5(n+1) | D、10(n+1) |
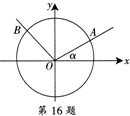 如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A (x1,yl),将射线OA按逆时针方向旋转
如图,角α的始边与x轴的非负半轴重合,终边与单位圆交于点A (x1,yl),将射线OA按逆时针方向旋转