题目内容
8. 在直角坐标系xOy中,设抛物线E:y2=2px(p>0)的焦点为F,准线为直线l,点A、B在直线l上,点M为抛物线E第一象限上的点,△ABM是边长为$\frac{8}{3}$$\sqrt{3}$的等边三角形,直线MF的倾斜角为60°.
在直角坐标系xOy中,设抛物线E:y2=2px(p>0)的焦点为F,准线为直线l,点A、B在直线l上,点M为抛物线E第一象限上的点,△ABM是边长为$\frac{8}{3}$$\sqrt{3}$的等边三角形,直线MF的倾斜角为60°.(1)求抛物线E的方程;
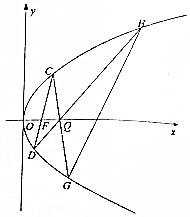
(2)如图,直线m过点F交抛物线E于C、D两点,Q(2,0),直线CQ、DQ分别交抛物线E于G、H两点,设直线CD、GH的斜率分别为k1、k2,求$\frac{{k}_{1}}{{k}_{2}}$的值.
分析 (I)由△ABM是边长为$\frac{8}{3}$$\sqrt{3}$的等边三角形,得|AB|=|AM|=|BMF|=4,
如图1,作MM′⊥l于点M′,FN⊥MM′于点N,由抛物线的定义知|MF|=|MM′,由|MN|=|MM′|-||NM′|=2,得p=|MN|;
(Ⅱ)设直线CD的方程为x=my+1,C(x1,y1),D(x2,y2),联立$\left\{\begin{array}{l}{x=my+1}\\{{y}^{2}=4x}\end{array}\right.$⇒y2-4my-4=0
得C的坐标$(\frac{{{y}_{1}}^{2}}{4},{y}_{1})$,kCQ=$\frac{4{y}_{1}}{{{y}_{1}}^{2}-8}$,写出直线CQ的方程,得G、H坐标即可.
解答 解:(I)∵△ABM是边长为$\frac{8}{3}$$\sqrt{3}$的等边三角形,∴|AB|=|AM|=|BMF|=4,
如图1,作MM′⊥l于点M′,FN⊥MM′于点N…(1分)
由抛物线的定义知|MF|=|MM′|=4,
∵直线MF的倾斜角为60°,∴∠MFx=∠FMM′=600
所以|MN|=|MM′|-||NM′|=2,所以p=|MN|=2…(3分)
所以抛物线E的方程y2=4x…(4分)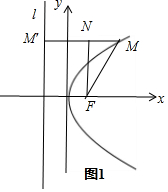
(II)设直线CD的方程为x=my+1,C(x1,y1),D(x2,y2)…(5分)
联立$\left\{\begin{array}{l}{x=my+1}\\{{y}^{2}=4x}\end{array}\right.$⇒y2-4my-4=0
△=16m2+16>0,y1+y2=4m,{y1y2=-4…(6分)
因为点C在抛物线E:y2=4x上,所以点C的坐标$(\frac{{{y}_{1}}^{2}}{4},{y}_{1})$,
所以kCQ=$\frac{4{y}_{1}}{{{y}_{1}}^{2}-8}$,…(7分)
所以直线CQ的方程为:y-0=$\frac{4{y}_{1}}{{{y}_{1}}^{2}-8}(x-2)$,即x=$\frac{{{y}_{1}}^{2}-8}{4{y}_{1}}y+2$,…(8分)
联立把x=$\frac{{{y}_{1}}^{2}-8}{4{y}_{1}}y+2$代入y2=4x,解得G($\frac{16}{{{y}_{1}}^{2}},-\frac{8}{{y}_{1}}$ ) 同理可得,H($\frac{16}{{{y}_{2}}^{2}},-\frac{8}{{y}_{2}}$),…(10分)
所以${k}_{1}=\frac{{y}_{1}-{y}_{2}}{\frac{{{y}_{1}}^{2}}{4}-\frac{{{y}_{2}}^{2}}{4}}=\frac{4}{{y}_{1}+{y}_{2}}$,
${k}_{2}=\frac{{y}_{H}-{y}_{G}}{{x}_{H}-{x}_{G}}=-\frac{{y}_{1}{y}_{2}}{2({y}_{1}+{y}_{2})}=\frac{2}{{y}_{1}+{y}_{2}}$…(11分)
所以$\frac{{k}_{1}}{{k}_{2}}=2$ …(12分)
点评 本题考查了抛物线的方程,及直线与抛物线的位置关系,属于中档题.

 名校课堂系列答案
名校课堂系列答案
| A. | $f(x)=\frac{{{e^x}-1}}{{{x^2}-1}}$ | B. | $f(x)=\frac{e^x}{{{x^2}-1}}$ | C. | $f(x)=\frac{{{x^3}+x+1}}{{{x^2}-1}}$ | D. | $f(x)=\frac{{{x^4}+x+1}}{{{x^2}-1}}$ |
| A. | -4 | B. | $-\frac{4}{5}$ | C. | $\frac{4}{5}$ | D. | 4 |
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\sqrt{3}$x | C. | y=±2x | D. | y=±$\sqrt{5}$x |
| A. | $\frac{-7-i}{5}$ | B. | $\frac{-7+i}{5}$ | C. | $\frac{7+i}{5}$ | D. | $\frac{7-i}{5}$ |