题目内容
9.在△ABC中,$\overrightarrow{BD}$=2$\overrightarrow{DC}$,$\overrightarrow{AB}$=m$\overrightarrow{AD}$+n$\overrightarrow{AC}$,则mn=-6.分析 由已知$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{BD}$=$\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}$,从而$\overrightarrow{AB}$=$\overrightarrow{AD}$-$\frac{2}{3}\overrightarrow{BC}$,由此能求出mn的值.
解答 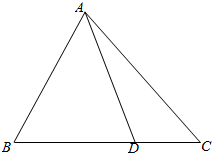 解:∵在△ABC中,$\overrightarrow{BD}$=2$\overrightarrow{DC}$,
解:∵在△ABC中,$\overrightarrow{BD}$=2$\overrightarrow{DC}$,
∴$\overrightarrow{AD}$=$\overrightarrow{AB}+\overrightarrow{BD}$=$\overrightarrow{AB}+\frac{2}{3}\overrightarrow{BC}$,
∴$\overrightarrow{AB}$=$\overrightarrow{AD}$-$\frac{2}{3}\overrightarrow{BC}$
=$\overrightarrow{AD}$-$\frac{2}{3}$($\overrightarrow{AC}-\overrightarrow{AB}$)
=$\overrightarrow{AD}-\frac{2}{3}\overrightarrow{AC}$+$\frac{2}{3}\overrightarrow{AB}$,
∴$\frac{1}{3}\overrightarrow{AB}$=$\overrightarrow{AD}-\frac{2}{3}\overrightarrow{AC}$,
∴$\overrightarrow{AB}$=3$\overrightarrow{AD}$-2$\overrightarrow{AC}$,
∵$\overrightarrow{AB}$=m$\overrightarrow{AD}$+n$\overrightarrow{AC}$,
∴m=3,n=-2.
∴mn=-6.
故答案为:-6.
点评 本题考查向量的线性运算,是基础题,解题时要认真审题,注意加法法则的合理运用.

| A. | 1 | B. | -1 | C. | $\sqrt{5}$ | D. | $\frac{\sqrt{5}}{5}$ |
| A. | $\frac{7}{15}$ | B. | $\frac{8}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
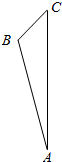 在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为[10°,50°].
在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为[10°,50°].