题目内容
19.已知|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=5,|$\overrightarrow{a}$+$\overrightarrow{b}$|=7.(1)求向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角θ;
(2)当向量k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$垂直时,求实数k的值.
分析 (1)对模两边平方,利用两个向量的数量积的定义解得cosθ=$\frac{1}{2}$,即可求出θ的度数;
(2)根据向量垂直,其数量积为0,即可求出k的值.
解答 解:(1)∵|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=5,|$\overrightarrow{a}$+$\overrightarrow{b}$|=7,
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|2=($\overrightarrow{a}$)2+($\overrightarrow{b}$)2+2$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2+2|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=9+25+30cosθ=47,
∴cosθ=$\frac{1}{2}$
∵0°≤θ≤180°,
∴θ=60°;
(2)∵向量k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$垂直,
∴(k$\overrightarrow{a}$+$\overrightarrow{b}$)($\overrightarrow{a}$-2$\overrightarrow{b}$)=0,
∴k|$\overrightarrow{a}$|2-2|$\overrightarrow{b}$|2+(1-2k)|$\overrightarrow{a}$||$\overrightarrow{b}$|cosθ=0,
即9k-50+(1-2k)×3×5×$\frac{1}{2}$=0,
解得k=-$\frac{85}{12}$.
点评 本题主要考查两个向量的数量积的定义,两个向量数量积的运算,向量的垂直的条件,根据三角函数的值求角,属于中档题

 同步练习强化拓展系列答案
同步练习强化拓展系列答案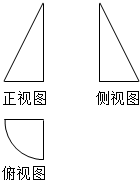 一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的$\frac{1}{4}$圆周和两条半径,则这个几何体的体积为( )
一个几何体的三视图如图所示,其中正视图与侧视图都是斜边长为2的直角三角形,俯视图是半径为1的$\frac{1}{4}$圆周和两条半径,则这个几何体的体积为( )| A. | $\frac{\sqrt{3}}{12}$π | B. | $\frac{\sqrt{3}}{6}$π | C. | $\frac{\sqrt{3}}{4}$π | D. | $\frac{\sqrt{3}}{3}$π |
| A. | 2$\sqrt{6}$ | B. | 2$\sqrt{7}$ | C. | $\sqrt{14}$ | D. | 4 |