题目内容
7.如图,在矩形ABCD中,AB=1,BC=$\sqrt{3}$,此矩形沿地面上一条直线滚动,在滚动过程中始终与地面垂直,设直线BC与地面所成的角为θ,矩形周边上最高点离地面的距离为f(θ),求: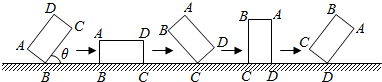
(1)θ的取值范围;
(2)函数f(θ)的解析式;
(3)函数f(θ)的值域.
分析 (1)根据BC与地面所成的角,是直线BC与平面所成的角,得出θ的取值范围;
(2)先求出∠DBC的大小,再作出图形,根据图形求出f(θ)的解析式;
(3)根据(2),结合三角函数的图象与性质,求出f(θ)的值域.
解答 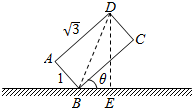 解:(1)BC与地面所成的角,是直线BC与地平面所成的角,
解:(1)BC与地面所成的角,是直线BC与地平面所成的角,
∴角θ的范围是[0,$\frac{π}{2}$];
(2)连接BD,Rt△BCD中,CD=AB=1,BC=AD=$\sqrt{3}$,
∴∠DBC=$\frac{π}{6}$;
过点D作地平面的垂线,垂足为E,如图所示;
在Rt△BDE中,∠DBE=θ+$\frac{π}{6}$,DB=2,
∴f(θ)=2sin(θ+$\frac{π}{6}$),(0≤θ≤$\frac{π}{2}$);
(3)由(2)知,当0≤θ≤$\frac{π}{2}$时,$\frac{π}{6}$≤θ≤$\frac{2π}{3}$,
∴$\frac{1}{2}$≤sin(θ+$\frac{π}{6}$)≤1,
∴1≤2sin(θ+$\frac{π}{6}$)≤2,
∴f(θ)的值域是[1,2].
点评 本题考查了三角函数的图象与性质的应用问题,也考查了数学建模的应用问题,是中档题.

练习册系列答案
相关题目
17.若角a的终边落在一,四象限及x轴的正半轴,则角a的集合为( )
| A. | {a|270°+k•360°<a<90°+k•360°,k∈Z} | B. | {a|-90°+k•360°<a<270°+k•360°,k∈Z} | ||
| C. | {a|-90°+k•360°<a<90°+k•360°,k∈Z} | D. | {a|-90°+k•720°<a<90°+k•720°,k∈Z} |
15.函数f(x)的定义域为{x∈R|x≠1},对定义域中的任意的x,都有f(2-x)=f(x),且当x<1时,f(x)=2x2-x,那么当x>1时,f(x)的递减区间是( )
| A. | $[\frac{5}{4},+∞)$ | B. | $(1,\frac{5}{4}]$ | C. | $[\frac{7}{4},+∞)$ | D. | $(1,\frac{7}{4})$ |
2.为分析学生初中升学的数学成绩对高一数学学习的影响,在高一年级随机抽取10名学生,了解他们的人学数学成绩和高一期末考试数学成绩如下表:
(1)画出散点图;
(2)对变量x与y进行相关性检验,如果x与y之间具有线性相关关系,求出回归直线方程.
(3)若某学生人学的数学成绩为80分,试估计他在高一期末考试中的数学成绩.
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 入学成绩(x/分) | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
| 高一期末成绩(y/分) | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(2)对变量x与y进行相关性检验,如果x与y之间具有线性相关关系,求出回归直线方程.
(3)若某学生人学的数学成绩为80分,试估计他在高一期末考试中的数学成绩.
12.已知圆C:x2+y2+ax-4=0上存在两点关于直线x-2y+3=0对称,则实数a的值( )
| A. | 8 | B. | -4 | C. | 6 | D. | 无法确定 |