题目内容
设数列{an}的前n项和为Sn,且满足Sn=2-an,n∈N*
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2nan,数列{bn}的前n项和为Tn,证明:Tn≥2.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=2nan,数列{bn}的前n项和为Tn,证明:Tn≥2.
考点:数列的求和,数列与不等式的综合
专题:等差数列与等比数列
分析:(Ⅰ)由已知条件推导出Sn-Sn-1=-an+an-1,由此得到{an}是以1为首项,
为公比的等比数列,从而求出an=(
)n-1.
(2)由bn=2nan=n(
)n-2=
,利用错位相减法能证明Tn≥2.
| 1 |
| 2 |
| 1 |
| 2 |
(2)由bn=2nan=n(
| 1 |
| 2 |
| n |
| 2n-2 |
解答:
(Ⅰ)解:当n=1时,a1=S1=1,
当n≥2时,Sn=2-an,Sn-1=2-an-1,
两式相减得:Sn-Sn-1=-an+an-1,
整理得2an=an-1,
∴
=
,(n≥2),
∴{an}是以1为首项,
为公比的等比数列,
∴an=(
)n-1.
(2)证明:bn=2nan=n(
)n-2=
,
∴Tn=
+
+
+…+
,①
Tn=
+
+
+…+
,②
①-②得:
Tn=
+
+
+
+…+
-
=2+
-
=4-
-
,
∴T=8-
-
=8-
,
∵Tn+1-Tn=(8-
)-(8-
)=
>0在n∈N*时恒成立,
即Tn+1>Tn,∴{Tn}单调递增,
∴{Tn}的最小值为T1=8-
=2,
∴Tn≥2.
当n≥2时,Sn=2-an,Sn-1=2-an-1,
两式相减得:Sn-Sn-1=-an+an-1,
整理得2an=an-1,
∴
| an |
| an-1 |
| 1 |
| 2 |
∴{an}是以1为首项,
| 1 |
| 2 |
∴an=(
| 1 |
| 2 |
(2)证明:bn=2nan=n(
| 1 |
| 2 |
| n |
| 2n-2 |
∴Tn=
| 1 |
| 2-1 |
| 2 |
| 20 |
| 3 |
| 2 |
| n |
| 2n-2 |
| 1 |
| 2 |
| 1 |
| 20 |
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
①-②得:
| 1 |
| 2 |
| 1 |
| 2-1 |
| 1 |
| 20 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-2 |
| n |
| 2n-1 |
=2+
1-
| ||
1-
|
| n |
| 2n-1 |
=4-
| 1 |
| 2n-2 |
| n |
| 2n-1 |
∴T=8-
| 1 |
| 2n-3 |
| n |
| 2n-2 |
| n+2 |
| 2n-2 |
∵Tn+1-Tn=(8-
| n+3 |
| 2n-1 |
| n+2 |
| 2n-2 |
| n+1 |
| 2n-1 |
即Tn+1>Tn,∴{Tn}单调递增,
∴{Tn}的最小值为T1=8-
| 3 |
| 2-1 |
∴Tn≥2.
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
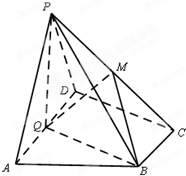 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=