题目内容
 如图,半径是3
如图,半径是3| 3 |
考点:与圆有关的比例线段
专题:推理和证明
分析:由已知得∠ABD=∠DAN=30°,∠ADB=90°,AB=6
,AD=3
,BD=9,由相交弦定理,得PA×PC=PD×PB,由此能求出结果.
| 3 |
| 3 |
解答:
解:∵半径是3
的⊙O中,AB是直径,MN是过点A的⊙O的切线,
AC,BD相交于点P,且∠DAN=30°,CP=2,PA=9,
∴∠ABD=∠DAN=30°,∠ADB=90°,
∴AB=6
,AD=3
,BD=9,
由相交弦定理,得PA×PC=PD×PB,
设PD=x,则PB=9-x,∴9×2=x(9-x),
解得x=3或x=6,
∴PD=6,PB=3或PD=3,PB=6(舍),
故PD=6.
故答案为:6.
| 3 |

AC,BD相交于点P,且∠DAN=30°,CP=2,PA=9,
∴∠ABD=∠DAN=30°,∠ADB=90°,
∴AB=6
| 3 |
| 3 |
由相交弦定理,得PA×PC=PD×PB,
设PD=x,则PB=9-x,∴9×2=x(9-x),
解得x=3或x=6,
∴PD=6,PB=3或PD=3,PB=6(舍),
故PD=6.
故答案为:6.
点评:本题考查与圆有关的线段长的求法,是中档题,解题时要认真审题,注意弦切角定理和相交弦定理的合理运用.

练习册系列答案
相关题目
已知向量
,
满足|
|=|
|=2,
与
的夹角为120°,则|
-
|的值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、1 | ||
B、2
| ||
C、3
| ||
| D、12 |
集合A={x∈N|x≤6},B={x∈R|x2-3x>0},则A∩B=( )
| A、{x|3≤x<6} |
| B、{3,4,5} |
| C、{x|3<x≤6} |
| D、{4,5,6} |
某几何体的三视图如图所示,则该几何体的表面积是( )


| A、90 | B、92 | C、98 | D、104 |
一个几何体的三视图尺寸如图,则该几何体的表面积为( )


A、4+8
| ||
| B、20 | ||
C、4+4
| ||
| D、12 |
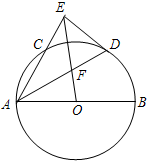 如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若