题目内容
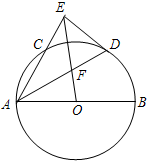 如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若| AC |
| AB |
| 3 |
| 5 |
| AF |
| FD |
考点:与圆有关的比例线段
专题:直线与圆
分析:连接OD,BC,设BC交OD于点M,则∠OAD=∠ODA,从而∠ODA=∠DAE,OD∥AE,又AC⊥BC,且DE⊥AC,从而BC∥DE.进而四边形CMDE为平行四边形,由此能求出
.
| AF |
| FD |
解答:
本小题满分(10分)
解:连接OD,BC,设BC交OD于点M.
∵OA=OD,∴∠OAD=∠ODA,
又∵∠OAD=∠DAE,∴∠ODA=∠DAE,
∴OD∥AE,又∵AC⊥BC,且DE⊥AC,∴BC∥DE.
∴四边形CMDE为平行四边形,∴CE=MD
由
=
,设AC=3x,AB=5x,则OM=
x,又OD=
x,
∴MD=
x-
x=x,∴AE=AC+CE=4x,
∵OD∥AE,∴
=
=
=
.
解:连接OD,BC,设BC交OD于点M.
∵OA=OD,∴∠OAD=∠ODA,
又∵∠OAD=∠DAE,∴∠ODA=∠DAE,
∴OD∥AE,又∵AC⊥BC,且DE⊥AC,∴BC∥DE.
∴四边形CMDE为平行四边形,∴CE=MD
由
| AC |
| AB |
| 3 |
| 5 |
| 3 |
| 2 |
| 5 |
| 2 |
∴MD=
| 5 |
| 2 |
| 3 |
| 2 |
∵OD∥AE,∴
| AF |
| FD |
| AE |
| OD |
| 4x | ||
|
| 8 |
| 5 |
点评:本题考查两线段比值的求法,是中档题,解题时要认真审题,注意圆的性质和平行四边形性质的合理运用.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
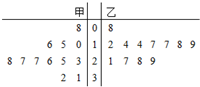 如图是某篮球联赛中,甲、乙两名运动员12个场次得分的茎叶图.设甲、乙两人得分的平均数分别为
如图是某篮球联赛中,甲、乙两名运动员12个场次得分的茎叶图.设甲、乙两人得分的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若
=(sin2x,cos2x),
=(sin2x,-cos2x),f(x)=
•
+4cos2x+2
sinxcosx.如果?m∈R,对?x∈R都有f(x)≥f(m),则f(m)等于( )
| a |
| b |
| a |
| b |
| 3 |
A、2+2
| ||
| B、3 | ||
| C、0 | ||
D、2-2
|
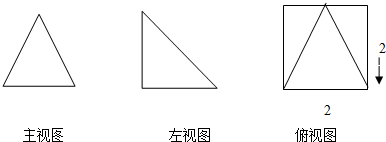
若空间几何体的三视图如图所示,则该几何体体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
| D、8 |
已知一个几何体的三视图如图所示,那么该几何体的表面积是( )


A、5+
| ||
| B、7 | ||
C、7+
| ||
| D、9 |
 如图,半径是
如图,半径是