题目内容
等差数列{an}的前n项和为Sn，若
=10，则am= ．
| S2m-1 |
| 2m-1 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：由等差数列的性质和求和公式可得S2m-1=（2m-1）am，代入已知式子可得am的值．
解答：
解：由等差数列的性质和求和公式可得：
S2m-1=
=
=（2m-1）am，
∵
=10，∴
=10，
∴am=10
故答案为：10
S2m-1=
| (2m-1)(a1+a2m-1) |
| 2 |
=
| (2m-1)•2am |
| 2 |
∵
| S2m-1 |
| 2m-1 |
| (2m-1)am |
| 2m-1 |
∴am=10
故答案为：10
点评：本题考查等差数列的求和公式和性质，属基础题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
若函数f（x）满足：?x1，x2∈[-1，1]，都有|f（x1）-f（x2）|≤|x1-x2|成立，则称f（x）∈Ψ．对于函数g（x）=x3-x，h（x）=
，有（ ）
|
| A、g（x）∈Ψ且h（x）∈Ψ |
| B、g（x）∈Ψ且h（x）∉Ψ |
| C、g（x）∉Ψ且h（x）∈Ψ |
| D、g（x）∉Ψ且h（x）∉Ψ |
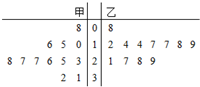如图是某篮球联赛中，甲、乙两名运动员12个场次得分的茎叶图．设甲、乙两人得分的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，半径是