题目内容
已知△ABC中，对于任意实数t，
=t（
+
），证明：点P始终在∠ACB的平分线上．
| CP |
| ||
|
|
| ||
|
|
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：在CA上取D，使|CD|=1，在CB上取E，使|CE|=1，作平行四边形CDFE，该平行四边形为菱形，所以对角线CF是∠ACB的平分线，并且
+
=
，所以
与
共线，所以点P始终在∠ACB的平分线上．
| ||
|
|
| ||
|
|
| CF |
| CP |
| CF |
解答：
证明：
，
都是单位向量，即长度为1，并且
与
同向，
与
同向，
如图，在AC上取|CD|=1，CB上取|CE|=1，作平行四边形CDFE；
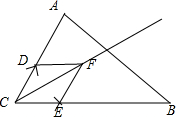则该平行四边形为菱形，
∴对角线CF为∠ACB的平分线，且
=
+
，t(
+
)与
共线；
∴点P始终在∠ACB的平分线上．
| ||
|
|
| ||
|
|
| ||
|
|
| CA |
| ||
|
|
| CB |
如图，在AC上取|CD|=1，CB上取|CE|=1，作平行四边形CDFE；
则该平行四边形为菱形，∴对角线CF为∠ACB的平分线，且
| CF |
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| CF |
∴点P始终在∠ACB的平分线上．
点评：考查单位向量的概念，向量加法的平行四边形法则，菱形对角线的性质，共线向量基本定理．
练习册系列答案
名校课堂系列答案
相关题目
如图：（1）将程序框图表示的函数写出来；