题目内容
设平面内互不相等的非零向量
、
满足|
|=1,
-
与
的夹角为150°,则
•
的最大值为 .
| a |
| b |
| a |
| a |
| b |
| b |
| a |
| b |
考点:平面向量数量积的运算
专题:三角函数的图像与性质,平面向量及应用
分析:设
=
,
=
,则
=
-
,由已知可得:B点为半径为1的圆上与OA不重合的动点,进而利用坐标法,结合三角函数的图象和性质,可得答案.
| a |
| OA |
| b |
| OB |
| BA |
| a |
| b |
解答:
解:设
=
,
=
,
则
=
-
,
∵|
|=1,
-
与
的夹角为150°,
∴△OAB中,OA=1,∠OBA=180°-30°,
由正弦定理可得:△OAB的半径为1,
则B点为圆上与OA不重合的动点,
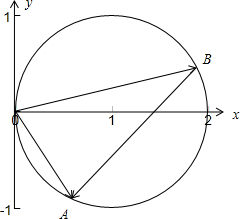
由上图可令
=
=(
,-
),
=
=(1+cosθ,sinθ)
则
•
=
+
cosθ-
sinθ=
+sin(
-θ),
当sin(
-θ)=1时,
•
的最大值为:
故答案为:
| a |
| OA |
| b |
| OB |
则
| BA |
| a |
| b |
∵|
| a |
| a |
| b |
| b |
∴△OAB中,OA=1,∠OBA=180°-30°,
由正弦定理可得:△OAB的半径为1,
则B点为圆上与OA不重合的动点,

由上图可令
| a |
| OA |
| 1 |
| 2 |
| ||
| 2 |
| b |
| OB |
则
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| π |
| 6 |
当sin(
| π |
| 6 |
| a |
| b |
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查的知识点是平面向量的数量积运算,正弦型函数的图象和性质,是三角函数与向量的综合应用,难度中档.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
设F1、F2是双曲线C:
-
=1(a>0,b>0)的两个焦点,P是C上一点,若|PF1|+|PF2|=6a,且△PF1F2最小内角的大小为30°,则双曲线C的渐近线方程是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、x±
| ||
| C、x±2y=0 | ||
| D、2x±y=0 |
若将函数f(x)=
sinx-
cosx的图象向右平移m个单位长度,得到的图象关于原点对称,则m=( )
| ||
| 4 |
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
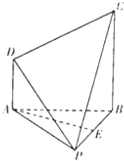 已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.
已知直角梯形ABCD与等腰直角△APB所在平面互相垂直,AD∥BC,∠APB=∠ABC=90°,AB=BC=2AD=2,E为PB的中点.